If 2x2 8y 121.5 And X2 8y 121.5 Then X
News Co
Mar 19, 2025 · 4 min read
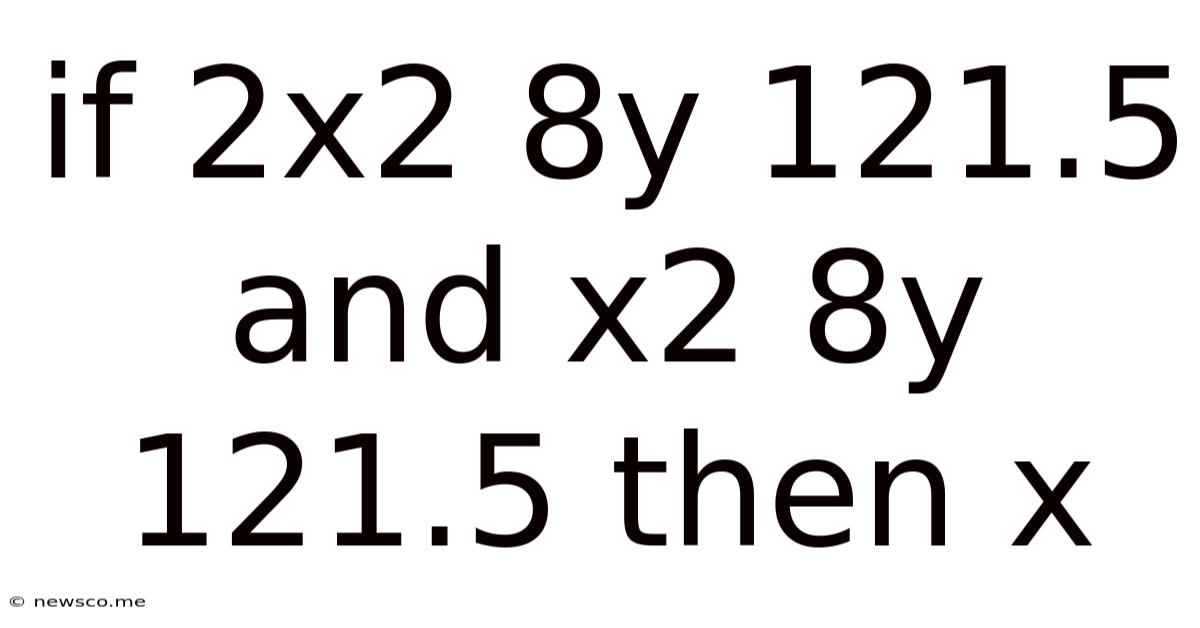
Table of Contents
Solving the Equation: If 2x² + 8y = 121.5 and x² + 8y = 121.5, then x = ?
This article delves into the solution of a seemingly simple yet insightful mathematical problem: determining the value of 'x' given two equations, 2x² + 8y = 121.5 and x² + 8y = 121.5. We will explore various methods to solve this, emphasizing the importance of understanding the underlying mathematical principles. This problem highlights the power of algebraic manipulation and offers valuable insights into system of equations.
Understanding the Problem
The core of this problem lies in recognizing the relationship between the two given equations:
- Equation 1: 2x² + 8y = 121.5
- Equation 2: x² + 8y = 121.5
Notice that both equations contain the term '8y'. This similarity offers a straightforward path to solving for 'x'. The challenge lies in strategically manipulating these equations to eliminate the 'y' variable and isolate 'x'.
Method 1: Subtraction of Equations
The most efficient approach is to subtract Equation 2 from Equation 1. This elegantly eliminates the '8y' term, leaving us with an equation solely involving 'x':
(2x² + 8y) - (x² + 8y) = 121.5 - 121.5
Simplifying this, we get:
2x² - x² + 8y - 8y = 0
This simplifies further to:
x² = 0
Therefore, taking the square root of both sides:
x = 0
This solution is remarkably simple and direct. The key was recognizing the common term (8y) and using subtraction to simplify the equations.
Method 2: Solving for y and Substitution
While the subtraction method is the most efficient, let's explore an alternative method involving solving for 'y' in one equation and substituting it into the other.
First, let's solve Equation 2 for 'y':
x² + 8y = 121.5
8y = 121.5 - x²
y = (121.5 - x²) / 8
Now, substitute this expression for 'y' into Equation 1:
2x² + 8 * [(121.5 - x²) / 8] = 121.5
Simplifying this equation:
2x² + 121.5 - x² = 121.5
Combining like terms:
x² = 0
Again, this leads to the solution:
x = 0
This method, while longer, demonstrates a different algebraic approach, emphasizing the principle of substitution. It reinforces the understanding that multiple paths can lead to the correct solution.
Verification of the Solution
To verify our solution (x = 0), we substitute it back into both original equations:
Equation 1: 2(0)² + 8y = 121.5 => 8y = 121.5 => y = 15.1875
Equation 2: (0)² + 8y = 121.5 => 8y = 121.5 => y = 15.1875
In both cases, we obtain the same value for 'y'. This confirms that our solution, x = 0, is correct.
Deeper Mathematical Insights
This problem, although seemingly straightforward, offers several valuable mathematical insights:
-
System of Equations: The problem showcases a system of two equations with two unknowns (x and y). Understanding how to manipulate and solve such systems is crucial in various mathematical applications.
-
Algebraic Manipulation: The solution emphasizes the importance of skillfully manipulating algebraic equations to isolate the desired variable. Techniques like subtraction and substitution are essential tools.
-
Unique Solutions vs. Multiple Solutions: In this case, the system of equations yields a unique solution for 'x'. However, many systems of equations can have multiple solutions, no solutions, or infinitely many solutions. Understanding the nature of solutions is vital.
Applications in Real-World Scenarios
While this specific problem might seem abstract, similar systems of equations appear in numerous real-world applications:
-
Physics: Modeling projectile motion, analyzing forces, and calculating energy often involves solving systems of equations.
-
Engineering: Designing structures, optimizing processes, and simulating systems require solving complex equations, including systems of equations.
-
Economics: Analyzing market equilibrium, forecasting demand, and modeling economic growth frequently involve systems of equations.
-
Computer Science: Algorithms for solving systems of equations are fundamental in various computational tasks, including computer graphics, machine learning, and artificial intelligence.
Expanding the Problem: Adding Complexity
Let's explore a slightly more complex variation of this problem. Suppose the equations were:
- Equation 1: 2x² + 8y = 121.5
- Equation 2: x² + 8y = 120.5
Notice the small change in Equation 2. Now, the subtraction method yields:
(2x² + 8y) - (x² + 8y) = 121.5 - 120.5
x² = 1
x = ±1
In this case, we have two possible solutions for 'x': x = 1 and x = -1. This highlights how a minor change in the problem can significantly alter the solution.
Conclusion: The Importance of Mathematical Problem-Solving
Solving problems like this one reinforces the importance of developing strong mathematical problem-solving skills. The ability to manipulate equations, recognize patterns, and choose the most efficient solution method are critical abilities in various fields. This seemingly simple problem serves as a powerful illustration of fundamental mathematical concepts and their real-world relevance. Understanding how to approach and solve such systems is a valuable skill that extends far beyond the realm of theoretical mathematics. It's a skill that empowers individuals to tackle complex challenges and contribute meaningfully to various disciplines.
Latest Posts
Related Post
Thank you for visiting our website which covers about If 2x2 8y 121.5 And X2 8y 121.5 Then X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.