If 5x X2 100 Then X Is Not
News Co
Apr 03, 2025 · 5 min read
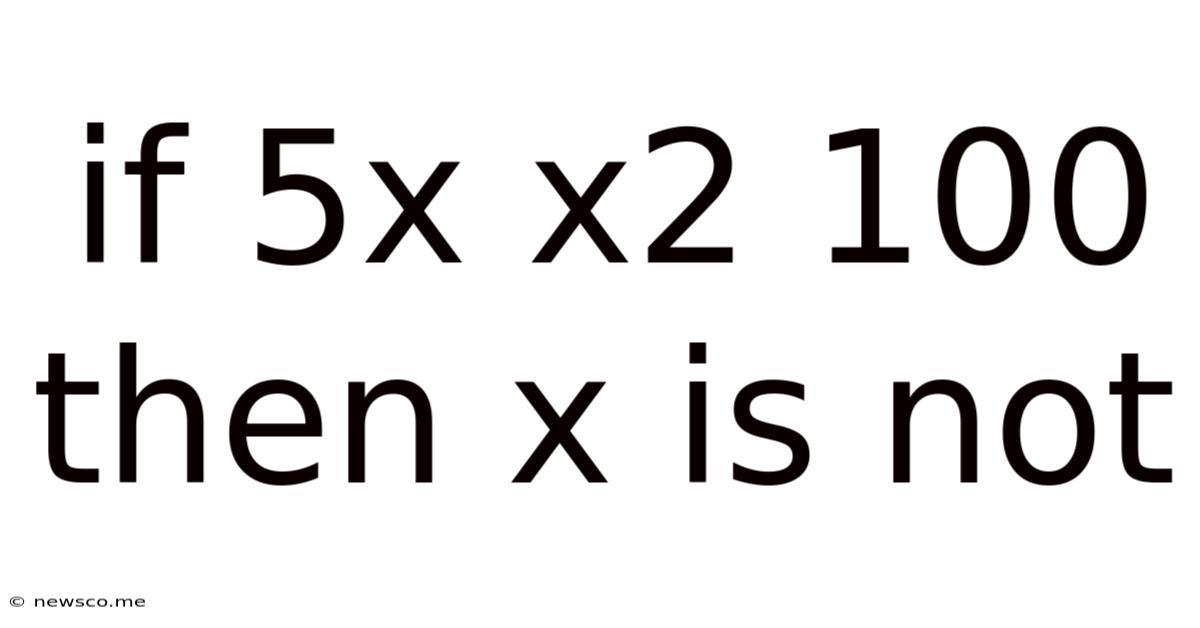
Table of Contents
- If 5x X2 100 Then X Is Not
- Table of Contents
- If 5x + x² = 100, then x is not… a simple solution? Let's delve deeper!
- Understanding Quadratic Equations
- Methods for Solving Quadratic Equations
- 1. Factoring
- 2. Quadratic Formula
- 3. Completing the Square
- Analyzing the Solutions
- The Significance of the Discriminant
- Graphical Representation
- Applications of Quadratic Equations
- Expanding the Exploration
- Latest Posts
- Related Post
If 5x + x² = 100, then x is not… a simple solution? Let's delve deeper!
This seemingly simple algebraic equation, 5x + x² = 100, presents a fascinating opportunity to explore various mathematical concepts beyond just finding the value of 'x'. While the immediate goal might seem straightforward – solving for 'x' – the true challenge lies in understanding the nature of the solutions and what they reveal about quadratic equations and their properties. This article will delve into the solution process, explore the characteristics of the solutions, and discuss the broader implications.
Understanding Quadratic Equations
Before jumping into the solution, let's establish a firm foundation. The equation 5x + x² = 100 is a quadratic equation. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (in this case, 'x') is 2. These equations have a standard form: ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero.
Our equation, 5x + x² = 100, isn't in standard form. To solve it effectively, we must rearrange it:
x² + 5x - 100 = 0
Now it's in the standard quadratic equation form, where a = 1, b = 5, and c = -100.
Methods for Solving Quadratic Equations
Several methods can be used to solve quadratic equations. Let's explore the most common ones:
1. Factoring
Factoring involves expressing the quadratic expression as a product of two linear expressions. If we can find two numbers that add up to 'b' (5 in our case) and multiply to 'c' (-100), we can factor the equation. In this case, the numbers 15 and -10 satisfy this condition (15 + (-10) = 5 and 15 * (-10) = -100).
Therefore, we can factor the equation as:
(x + 15)(x - 10) = 0
This implies that either (x + 15) = 0 or (x - 10) = 0. Solving these linear equations gives us two potential solutions:
- x = -15
- x = 10
2. Quadratic Formula
The quadratic formula is a powerful tool that provides a solution for any quadratic equation, regardless of its factorability. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = 5, c = -100), we get:
x = [-5 ± √(5² - 4 * 1 * -100)] / (2 * 1) x = [-5 ± √(25 + 400)] / 2 x = [-5 ± √425] / 2 x = [-5 ± 5√17] / 2
This gives us the same solutions as factoring, albeit in a slightly different form:
- x = (-5 + 5√17) / 2 ≈ 10
- x = (-5 - 5√17) / 2 ≈ -15
3. Completing the Square
Completing the square is another method to solve quadratic equations. This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. While effective, it's often more complex than factoring or using the quadratic formula for simpler equations.
Analyzing the Solutions
We've found two solutions for x: 10 and -15. The question posed, "If 5x + x² = 100, then x is not...", implies there are values 'x' cannot be. Let's analyze this:
-
x is not any other number: The quadratic equation has only two solutions. No other value of 'x' will satisfy the equation.
-
x is not the solution to a different equation: The solutions are specific to this particular quadratic equation. They wouldn't be the solutions for, say, x² + 5x - 101 = 0.
-
x is not a complex number (in this case): The discriminant (b² - 4ac) is positive (425), indicating that the solutions are real numbers. If the discriminant were negative, the solutions would be complex numbers.
The Significance of the Discriminant
The discriminant (b² - 4ac) holds significant importance in understanding the nature of the quadratic equation's solutions.
- Discriminant > 0: Two distinct real roots (as in our case).
- Discriminant = 0: One real root (a repeated root).
- Discriminant < 0: Two complex roots (roots involving the imaginary unit 'i').
The discriminant provides crucial information about the parabola represented by the quadratic equation. A positive discriminant means the parabola intersects the x-axis at two distinct points (the roots). A zero discriminant means the parabola touches the x-axis at one point, and a negative discriminant means the parabola doesn't intersect the x-axis at all.
Graphical Representation
Visualizing the equation graphically helps solidify the understanding of its solutions. Plotting the function y = x² + 5x - 100 will reveal a parabola that intersects the x-axis at x = -15 and x = 10. These points of intersection represent the solutions to the equation x² + 5x - 100 = 0. The parabola's vertex represents the minimum value of the function.
Applications of Quadratic Equations
Quadratic equations have widespread applications across various fields:
- Physics: Modeling projectile motion, calculating the trajectory of objects under gravity.
- Engineering: Designing structures, calculating forces and stresses.
- Economics: Optimizing production, determining the equilibrium price in market models.
- Computer Graphics: Creating curved shapes and animations.
Expanding the Exploration
This in-depth analysis of the simple equation 5x + x² = 100 has broadened our understanding beyond merely finding the values of 'x'. We've explored the fundamentals of quadratic equations, various solution methods, the significance of the discriminant, and the graphical representation. Furthermore, we touched on the extensive applications of these equations in various fields.
This detailed explanation aims to be more than just a step-by-step solution; it aims to foster a deeper comprehension of the underlying mathematical principles. By understanding the "why" behind the solution, we can better appreciate the elegance and power of mathematics. Remember that mathematical exploration extends far beyond obtaining the answer; the journey itself is where true learning lies.
Latest Posts
Related Post
Thank you for visiting our website which covers about If 5x X2 100 Then X Is Not . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.