If A Equals B And B Equals C
News Co
May 07, 2025 · 5 min read
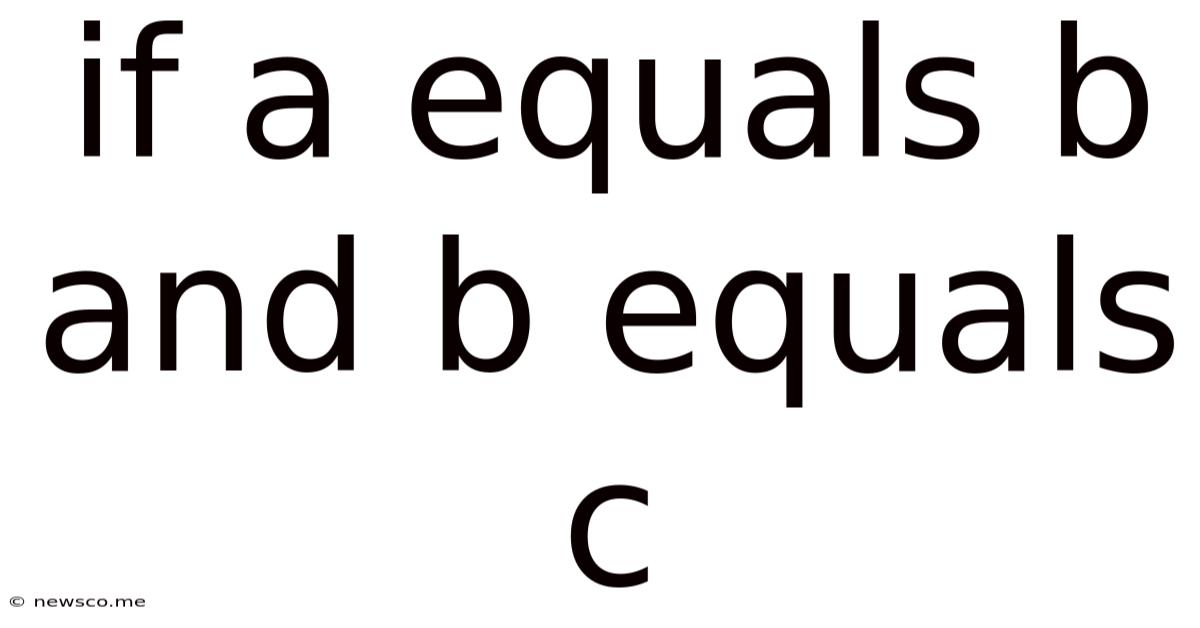
Table of Contents
If A Equals B, and B Equals C: Exploring Transitive Properties and Their Applications
The seemingly simple statement, "If A equals B, and B equals C, then A equals C," underlies a fundamental concept in mathematics and logic known as the transitive property. While its simplicity might initially mislead, this principle has far-reaching implications across numerous fields, influencing everything from basic arithmetic to complex computer algorithms and even philosophical arguments. This article delves into the transitive property, exploring its definition, applications, and the subtle nuances that can arise when dealing with its different forms and interpretations.
Understanding the Transitive Property
At its core, the transitive property states that if a relationship holds between two elements, and the same relationship holds between a second element and a third, then that relationship also holds between the first and third elements. This is most commonly expressed mathematically as:
If A = B and B = C, then A = C.
This specific instance refers to equality, but the transitive property extends beyond simple equivalence. It applies to various relationships, including:
- Less than (<): If A < B and B < C, then A < C.
- Greater than (>): If A > B and B > C, then A > C.
- Less than or equal to (≤): If A ≤ B and B ≤ C, then A ≤ C.
- Greater than or equal to (≥): If A ≥ B and B ≥ C, then A ≥ C.
- Set Inclusion (⊂): If A ⊂ B and B ⊂ C, then A ⊂ C.
The transitive property is a cornerstone of equivalence relations. An equivalence relation is a relationship that is reflexive (A = A), symmetric (if A = B, then B = A), and transitive. These properties ensure a consistent and predictable way to group elements based on shared characteristics. For instance, consider the relationship "is congruent to" for geometric shapes. If shape A is congruent to shape B, and shape B is congruent to shape C, then shape A is congruent to shape C.
Applications of the Transitive Property
The transitive property's influence extends far beyond the realm of pure mathematics. It plays a crucial role in various fields, including:
1. Computer Science and Algorithms
Many algorithms rely heavily on the transitive property for efficient data processing. Consider graph theory, where the transitive property is essential for finding shortest paths (e.g., using Dijkstra's algorithm) or determining connectivity in networks. If node A is connected to node B, and node B is connected to node C, then A is indirectly connected to C. This understanding is fundamental in network routing, social network analysis, and database management.
2. Logic and Reasoning
In formal logic, the transitive property is a crucial rule of inference. It allows us to deduce new conclusions from existing premises. For example, if we know "All men are mortal" (A) and "Socrates is a man" (B), then we can transitively conclude that "Socrates is mortal" (C). This type of deductive reasoning is essential in constructing valid arguments and proofs.
3. Geometry and Measurement
In geometry, the transitive property is inherent in comparing lengths, angles, and areas. If line segment AB has the same length as line segment BC, and line segment BC has the same length as line segment CD, then AB has the same length as CD. This applies similarly to angles and areas, ensuring consistency in geometric calculations and proofs.
4. Real-World Applications
The transitive property subtly impacts our daily lives. Think about comparing prices. If product A costs the same as product B, and product B costs the same as product C, we intuitively understand that product A and C cost the same. Similar logic applies to comparing weights, temperatures, or any measurable quantity.
Intransitive Relations and Exceptions
It is important to acknowledge that not all relationships are transitive. A relationship that does not satisfy the transitive property is called intransitive. Consider the relationship "is taller than." If person A is taller than person B, and person B is taller than person C, then person A is indeed taller than person C. However, this relationship is transitive.
However, consider the relationship "is a sibling of." If A is a sibling of B, and B is a sibling of C, it does not necessarily mean A is a sibling of C (A and C could be half-siblings, for example). This relationship is therefore intransitive, highlighting the importance of considering the specific nature of the relationship when applying (or avoiding) the transitive property. Another example of an intransitive relation is the “beats” relation in rock-paper-scissors. Rock beats scissors, scissors beats paper, but rock does not beat paper.
Circular Relationships: A special case emerges when we encounter circular relationships. If A = B, B = C, and C = A, this forms a closed loop or cycle. While seemingly counterintuitive, such circular relationships can be perfectly valid within specific contexts, such as in certain mathematical structures or when modeling cyclical processes.
The Transitive Property and Sets
The transitive property has a particularly interesting application in set theory. A set is said to be transitive if, for every element x in the set, every element of x is also in the set. In simpler terms, if a set contains another set, then it must also contain all the elements of that nested set. This concept of transitive sets is crucial in advanced set theory and foundational mathematics.
Conclusion
The transitive property, while seemingly straightforward, underpins a significant portion of mathematical and logical reasoning. Its applications span numerous fields, contributing to the development of algorithms, the construction of valid arguments, and the understanding of complex systems. Understanding the transitive property and its limitations, including the existence of intransitive relations, is essential for anyone working with mathematical or logical concepts. By appreciating its fundamental role, we gain a deeper insight into the structure and interconnectedness of information across diverse disciplines. This understanding empowers us to build stronger arguments, design more efficient algorithms, and make more informed decisions in a world governed by logic and relationships. The next time you encounter a comparison, consider the subtle yet powerful influence of the transitive property, quietly working behind the scenes to connect ideas and build our understanding of the world around us.
Latest Posts
Latest Posts
-
What Is The Length Of Rounded To The Nearest Tenth
May 08, 2025
-
Do The Diagonals Of A Square Bisect Each Other
May 08, 2025
-
Describe The Relationship Between Equations And The Properties Of Equality
May 08, 2025
-
Half Of 3 3 4 Inches
May 08, 2025
-
Select All Of The Following That Are Linear Functions
May 08, 2025
Related Post
Thank you for visiting our website which covers about If A Equals B And B Equals C . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.