If X 12y 210 And X 6y 90 Then X
News Co
Mar 23, 2025 · 4 min read
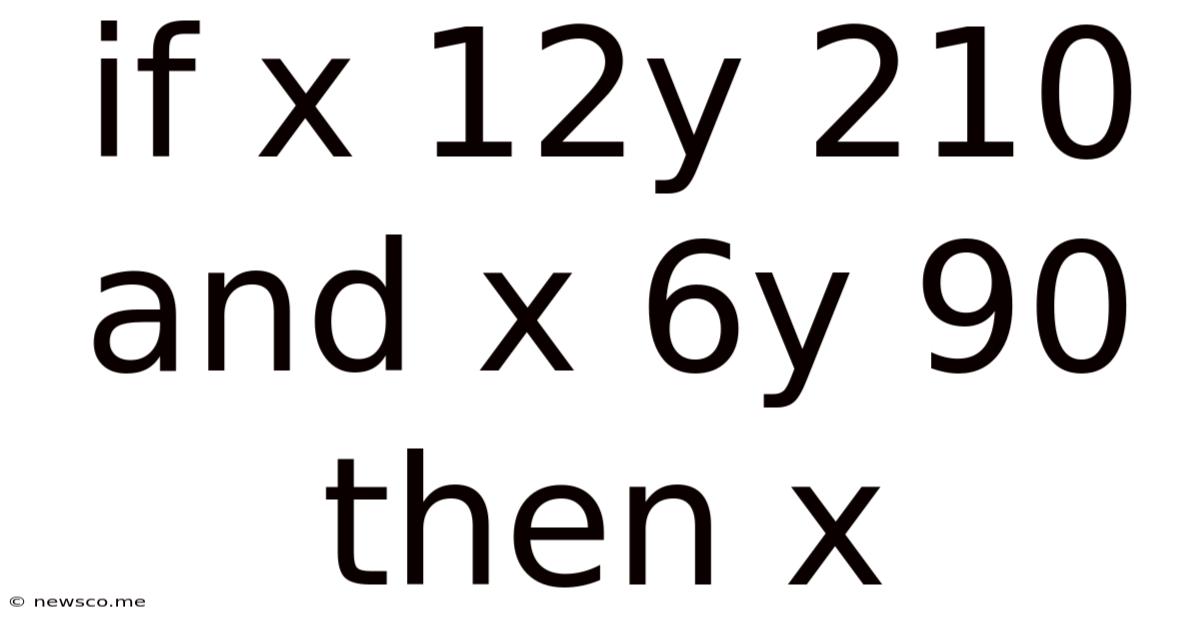
Table of Contents
Solving Simultaneous Equations: Finding the Value of x When x + 12y = 210 and x + 6y = 90
This article will guide you through the process of solving a system of simultaneous linear equations to find the value of 'x'. We'll be tackling a specific problem: x + 12y = 210 and x + 6y = 90. We'll explore various methods, explaining each step in detail, making this a comprehensive guide for students and anyone interested in mastering this fundamental mathematical concept.
Understanding Simultaneous Equations
Simultaneous equations, also known as systems of equations, involve two or more equations with the same variables. The goal is to find the values of the variables that satisfy all equations simultaneously. There are several methods to solve these equations, and the best method often depends on the specific equations. For our problem, we'll explore two common methods: elimination and substitution.
Method 1: Elimination Method
The elimination method focuses on eliminating one variable by adding or subtracting the equations. This requires manipulating the equations to make the coefficients of one variable opposites.
1. Identify the Variable to Eliminate:
In our equations, x + 12y = 210 and x + 6y = 90, both equations have 'x' with a coefficient of 1. This makes 'x' a convenient variable to eliminate.
2. Make Coefficients Opposites:
To eliminate 'x', we need to make the coefficients of 'x' opposites. Since both coefficients are currently 1, we can multiply the second equation by -1:
-1 * (x + 6y = 90) becomes -x - 6y = -90
3. Add the Equations:
Now, add the modified second equation to the first equation:
(x + 12y = 210) + (-x - 6y = -90)
Notice that the 'x' terms cancel out:
6y = 120
4. Solve for y:
Divide both sides by 6:
y = 20
5. Substitute and Solve for x:
Now that we know y = 20, substitute this value into either of the original equations to solve for x. Let's use the second equation:
x + 6(20) = 90
x + 120 = 90
x = 90 - 120
x = -30
Therefore, using the elimination method, we find that x = -30 and y = 20.
Method 2: Substitution Method
The substitution method involves solving one equation for one variable and substituting that expression into the other equation.
1. Solve One Equation for One Variable:
Let's solve the second equation (x + 6y = 90) for x:
x = 90 - 6y
2. Substitute into the Other Equation:
Substitute this expression for x (90 - 6y) into the first equation (x + 12y = 210):
(90 - 6y) + 12y = 210
3. Solve for y:
Simplify and solve for y:
90 + 6y = 210
6y = 210 - 90
6y = 120
y = 20
4. Substitute and Solve for x:
Substitute the value of y (20) back into either of the original equations or the expression we derived for x (x = 90 - 6y):
x = 90 - 6(20)
x = 90 - 120
x = -30
Therefore, using the substitution method, we also find that x = -30 and y = 20.
Verifying the Solution
It's always a good practice to verify your solution by substituting the values of x and y back into both original equations:
Equation 1: x + 12y = 210
-30 + 12(20) = -30 + 240 = 210 (Correct)
Equation 2: x + 6y = 90
-30 + 6(20) = -30 + 120 = 90 (Correct)
Both equations are satisfied, confirming that our solution x = -30 and y = 20 is accurate.
Applications of Simultaneous Equations
Simultaneous equations are crucial in various fields, including:
- Physics: Solving problems involving forces, motion, and electricity.
- Engineering: Designing structures, analyzing circuits, and modeling systems.
- Economics: Analyzing market equilibrium, supply and demand, and economic models.
- Chemistry: Determining the composition of mixtures and calculating reaction yields.
- Computer Science: Solving optimization problems and developing algorithms.
Advanced Techniques for Solving Simultaneous Equations
While elimination and substitution are fundamental methods, more complex systems might require more advanced techniques:
- Matrix methods: Using matrices and determinants to solve systems of equations efficiently, especially for larger systems.
- Graphical methods: Plotting the equations on a graph and finding the point of intersection (this is less precise for larger systems).
- Iterative methods: Using iterative algorithms to approximate the solution, particularly useful for non-linear systems.
Conclusion
Solving simultaneous equations is a fundamental skill in mathematics with broad applications across various disciplines. This article has provided a detailed explanation of two common methods – elimination and substitution – demonstrating how to solve a specific system of equations and verify the solution. Mastering these methods builds a strong foundation for tackling more complex mathematical problems and understanding their real-world applications. Remember to always check your solution to ensure accuracy! Understanding the underlying concepts and practicing regularly will significantly enhance your ability to solve simultaneous equations efficiently and effectively. The key is to choose the method that best suits the specific equations, and always double-check your answers!
Latest Posts
Related Post
Thank you for visiting our website which covers about If X 12y 210 And X 6y 90 Then X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.