Integral Of 1 1 T 2
News Co
May 02, 2025 · 5 min read
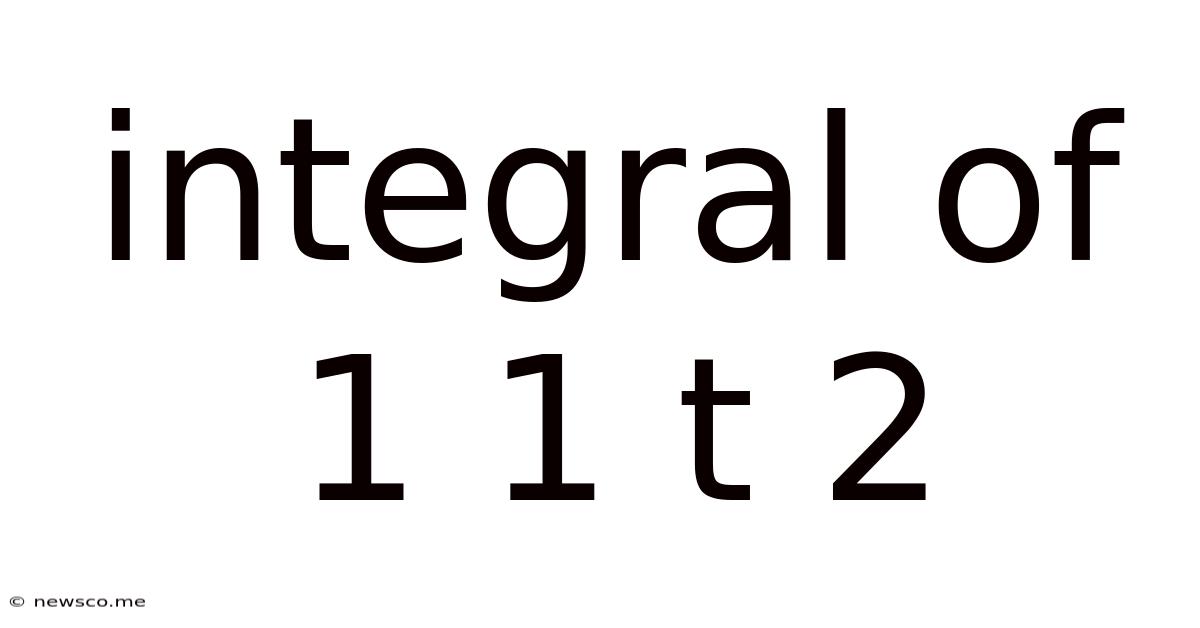
Table of Contents
The Definite Integral of 1/(1+t²) and its Applications
The integral ∫ 1/(1+t²) dt is a fundamental integral in calculus, with far-reaching applications in various fields. This integral is particularly significant because it directly relates to the inverse tangent function, also known as arctangent (arctan). Understanding this integral involves not only the mechanics of integration but also its geometric interpretation and practical uses. This comprehensive guide will delve into the intricacies of this integral, exploring its derivation, applications, and significance in different contexts.
Understanding the Integral: ∫ 1/(1+t²) dt
The expression ∫ 1/(1+t²) dt represents the indefinite integral of the function 1/(1+t²). This means we are looking for a function whose derivative is 1/(1+t²). The solution to this integral is remarkably simple and elegant:
∫ 1/(1+t²) dt = arctan(t) + C
where 'C' is the constant of integration. This constant is crucial because the derivative of a constant is zero. Thus, adding any constant to arctan(t) will still result in a derivative of 1/(1+t²).
Deriving the Integral: A Trigonometric Approach
The derivation of this integral often involves a clever substitution using trigonometric functions. Let's explore this method:
-
Substitution: Let's substitute t = tan(θ). This implies that dt = sec²(θ) dθ.
-
Substitution into the Integral: Substituting these values into the original integral, we get:
∫ 1/(1 + tan²(θ)) * sec²(θ) dθ
-
Trigonometric Identity: Recall the Pythagorean trigonometric identity: 1 + tan²(θ) = sec²(θ). Substituting this into the integral simplifies the expression:
∫ 1/sec²(θ) * sec²(θ) dθ = ∫ 1 dθ
-
Integration: The integral of 1 with respect to θ is simply θ.
-
Back-Substitution: Since t = tan(θ), we can rewrite θ as arctan(t). Therefore, the integral becomes:
arctan(t) + C
This derivation elegantly demonstrates the connection between the integral 1/(1+t²) and the arctangent function.
Geometric Interpretation: Area Under the Curve
The definite integral of a function represents the area under its curve between specified limits. For the function 1/(1+t²), the definite integral from a to b, ∫<sub>a</sub><sup>b</sup> 1/(1+t²) dt, represents the area under the curve of 1/(1+t²) between t = a and t = b. This area can be calculated using the antiderivative:
∫<sub>a</sub><sup>b</sup> 1/(1+t²) dt = arctan(b) - arctan(a)
This provides a powerful geometric interpretation of the integral. For example, the integral from 0 to 1, ∫<sub>0</sub><sup>1</sup> 1/(1+t²) dt, represents the area under the curve of 1/(1+t²) from t = 0 to t = 1. This area is numerically equal to arctan(1) - arctan(0) = π/4.
Applications of the Integral: Real-World Significance
The integral ∫ 1/(1+t²) dt finds extensive application across various fields:
1. Calculus and Analysis:
- Calculating Areas: As discussed above, this integral is crucial for calculating the area under the curve of 1/(1+t²). This extends to more complex functions involving this expression as a component.
- Solving Differential Equations: This integral frequently appears as a solution to various differential equations, particularly those related to harmonic motion and other oscillatory systems.
- Series Expansions: The arctangent function can be expressed as an infinite series, which is often derived from the integral representation. This series is valuable in numerical approximations and analysis.
2. Physics:
- Projectile Motion: This integral is relevant in analyzing projectile trajectories, specifically calculating the angle of elevation or trajectory parameters.
- Electric Fields: In electrostatics, the integral plays a role in calculating the electric field produced by certain charge distributions.
- Optics: The integral can be used in optical calculations, particularly in situations involving refraction and diffraction of light.
3. Engineering:
- Signal Processing: This integral appears in the context of Fourier transforms, which are fundamental tools in signal processing for analyzing and manipulating signals.
- Control Systems: In control systems engineering, the arctangent function and its integral form are utilized in modeling and analysis of feedback control systems.
4. Statistics and Probability:
- Probability Distributions: The integral can be part of calculating probabilities associated with certain probability distributions.
5. Computer Graphics and Game Development:
- Rotation and Transformations: The arctangent function, directly derived from this integral, is frequently used in computer graphics and game development for calculating angles and rotations of objects in two and three-dimensional spaces.
- Camera Positioning: Determining camera angles and perspective often involves computations related to arctangent.
Beyond the Basics: Exploring Related Integrals
Understanding ∫ 1/(1+t²) dt provides a foundation for tackling more complex integrals. These integrals often involve variations of the basic form or appear as part of more intricate integrands. Some examples include:
- ∫ 1/(a² + t²) dt: This integral is a simple extension, solvable by a substitution (let u = t/a). The solution involves a scaling factor: (1/a) arctan(t/a) + C.
- Integrals involving rational functions: Integrals with rational functions (ratios of polynomials) can sometimes be simplified or solved using partial fraction decomposition, where the 1/(1+t²) term or its variations might emerge.
- Integrals involving the arctangent function: Evaluating integrals involving arctangent often requires integration by parts or other advanced techniques.
Conclusion: A Fundamental Building Block
The seemingly simple integral ∫ 1/(1+t²) dt is a surprisingly versatile and powerful tool in mathematics and its various applications. Its connection to the arctangent function, its geometric interpretation as area under a curve, and its wide-ranging practical uses demonstrate its fundamental importance. Mastering this integral not only enhances your understanding of calculus but also equips you with a valuable tool for solving problems in diverse scientific and engineering domains. Through exploring its derivation, geometric meaning, and real-world applications, we have gained a deeper appreciation for this essential element of integral calculus. Further exploration into more complex integrals and their applications will build upon this foundation, expanding your mathematical capabilities and problem-solving skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about Integral Of 1 1 T 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.