Integral Of Cos X Sin X
News Co
May 07, 2025 · 5 min read
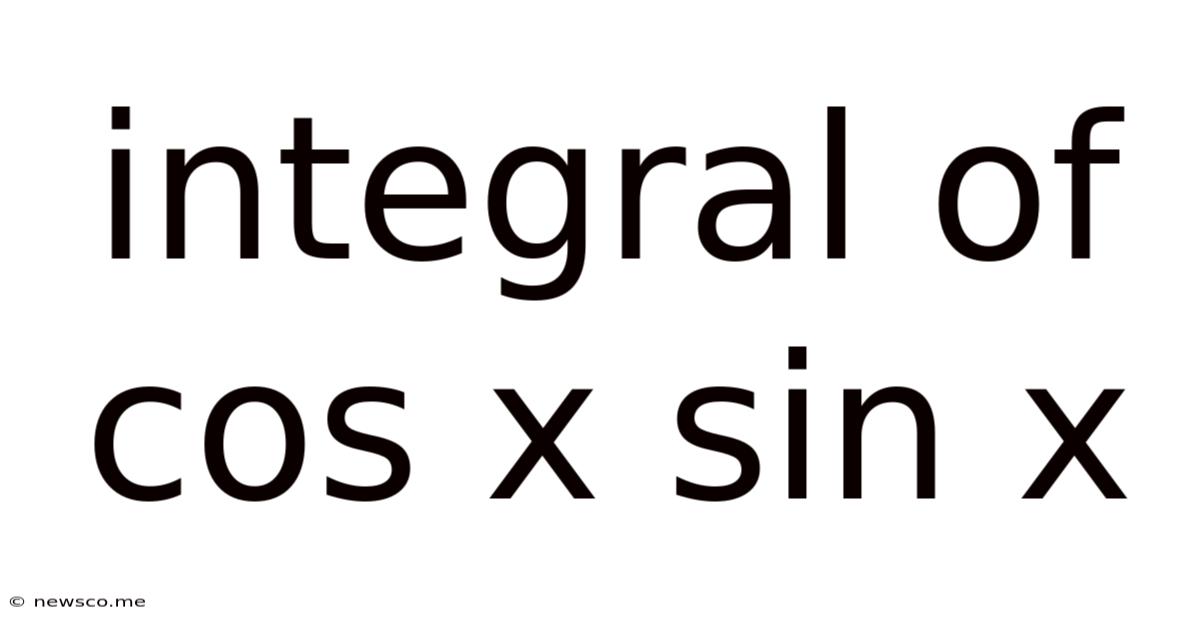
Table of Contents
Evaluating the Integral of cos x sin x: A Comprehensive Guide
The integral ∫cos x sin x dx is a classic example of a trigonometric integral that appears frequently in calculus. Its solution involves a straightforward application of substitution, making it an excellent problem for understanding integration techniques. This comprehensive guide will not only show you how to solve this integral but also explore various approaches, delve into the underlying principles, and provide you with a solid foundation for tackling more complex trigonometric integrals.
Understanding the Problem: ∫cos x sin x dx
Our goal is to find the antiderivative of the function f(x) = cos x sin x. This means we're searching for a function F(x) such that its derivative, F'(x), equals cos x sin x. We'll explore several methods to achieve this.
Method 1: u-Substitution – The Most Efficient Approach
The most efficient and straightforward method for solving this integral is u-substitution. This powerful technique allows us to simplify complex integrals by substituting a portion of the integrand with a new variable.
Steps:
-
Choose your substitution: Let's choose u = sin x. This is a good choice because the derivative of sin x is cos x, which is also present in the integrand.
-
Find du: Differentiating u = sin x with respect to x gives us du = cos x dx.
-
Substitute: Replace sin x with u and cos x dx with du in the original integral:
∫cos x sin x dx becomes ∫u du
-
Integrate: The integral of u with respect to u is a simple power rule integration:
∫u du = (1/2)u² + C, where C is the constant of integration.
-
Substitute back: Replace u with sin x to express the result in terms of the original variable x:
(1/2)u² + C = (1/2)(sin x)² + C
Therefore, the integral of cos x sin x is (1/2)(sin x)² + C.
Method 2: Using Trigonometric Identities – An Alternate Approach
Another approach involves using trigonometric identities to simplify the integrand before integration. We can use the double angle identity for sine:
sin(2x) = 2sin x cos x
Rearranging this identity gives:
sin x cos x = (1/2)sin(2x)
Now, we can substitute this into our original integral:
∫cos x sin x dx = ∫(1/2)sin(2x) dx
This integral is easily solved using a simple u-substitution (let u = 2x, then du = 2dx):
∫(1/2)sin(2x) dx = (1/2) ∫sin(u) (du/2) = (1/4) ∫sin(u) du = -(1/4)cos(u) + C
Substituting back u = 2x, we get:
-(1/4)cos(2x) + C
This might seem different from our previous result, but remember that trigonometric identities can lead to equivalent expressions. Using the double angle identity for cosine, cos(2x) = 1 - 2sin²(x), we can show that -(1/4)cos(2x) + C is indeed equivalent to (1/2)sin²(x) + C (apart from a constant).
Understanding the Constant of Integration (C)
The constant of integration, C, is crucial. It represents a family of antiderivatives, as the derivative of a constant is always zero. Adding any constant to (1/2)(sin x)² will not change its derivative, meaning all these functions are valid antiderivatives. The specific value of C depends on the initial conditions or boundary conditions of a particular problem.
Applications of the Integral of cos x sin x
This seemingly simple integral has applications in various fields:
-
Physics: It appears in calculations involving oscillatory motion, such as simple harmonic motion, where sine and cosine functions describe displacement and velocity.
-
Engineering: Similar to physics, it's used in analyzing vibrations and waves in structures and systems.
-
Signal Processing: Sine and cosine functions are fundamental in representing signals, and this integral plays a role in analyzing signal properties.
-
Probability and Statistics: In probability density functions, trigonometric functions can appear, and their integrals are crucial for calculating probabilities.
Expanding Your Understanding: More Complex Trigonometric Integrals
The techniques used to solve ∫cos x sin x dx serve as a foundation for tackling more complex trigonometric integrals. These often involve using a combination of:
-
Trigonometric identities: Mastering identities like the double-angle formulas, sum-to-product formulas, and product-to-sum formulas is crucial.
-
u-substitution: This remains a powerful tool for simplifying integrals.
-
Integration by parts: This technique is essential when dealing with integrals involving products of trigonometric and other functions.
-
Partial fraction decomposition: This method helps when the integrand is a rational function involving trigonometric functions.
Practice Problems to Solidify Your Understanding
To reinforce your understanding, try solving these related integrals:
- ∫sin x cos²x dx
- ∫sin²x cos x dx
- ∫sin x cos x sin(2x) dx
- ∫tan x sec²x dx
- ∫cos³x sin x dx
By tackling these problems, you’ll gain valuable practice and further develop your proficiency in solving trigonometric integrals. Remember to choose appropriate substitutions and apply the necessary trigonometric identities strategically.
Conclusion: Mastering Trigonometric Integration
The integral of cos x sin x, while seemingly simple, provides a valuable introduction to the techniques used to solve a wide range of trigonometric integrals. By mastering u-substitution, trigonometric identities, and other integration methods, you can confidently tackle more complex problems. Consistent practice and a deep understanding of these principles are essential for success in calculus and its applications in various scientific and engineering disciplines. Remember to always check your work and consider alternative methods to ensure accuracy and deepen your understanding. The constant exploration and application of these techniques will solidify your understanding and prepare you for more advanced topics in calculus.
Latest Posts
Related Post
Thank you for visiting our website which covers about Integral Of Cos X Sin X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.