Integral Sin X From 0 To Pi
News Co
Apr 18, 2025 · 5 min read
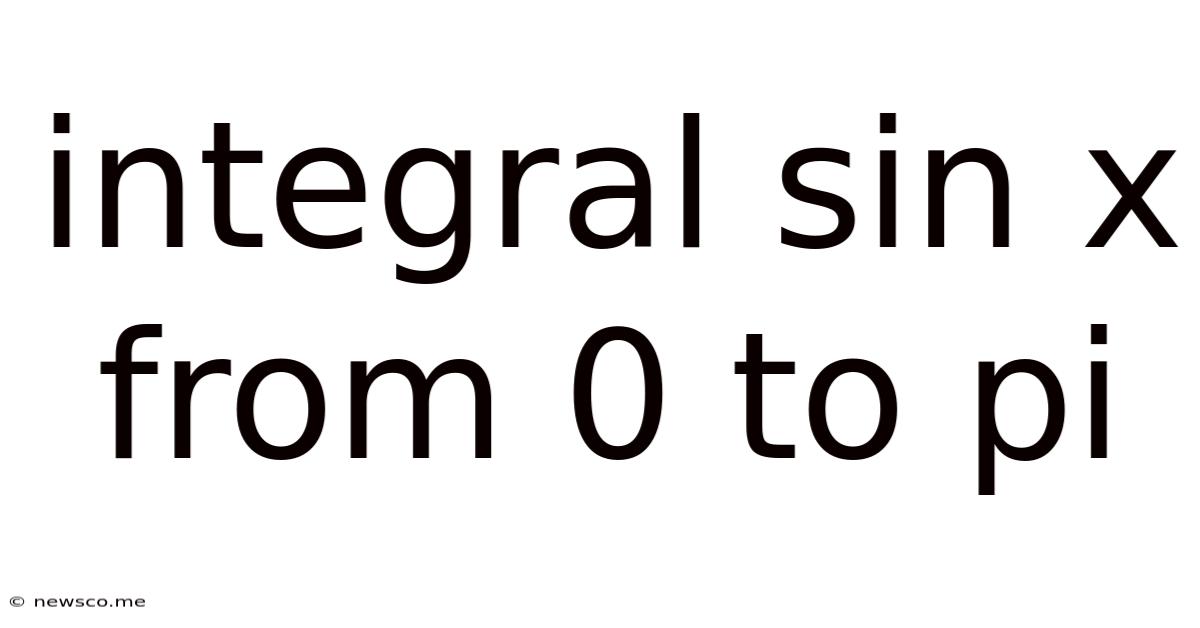
Table of Contents
The Definite Integral of sin x from 0 to π: A Comprehensive Guide
The definite integral of sin x from 0 to π, represented as ∫₀^π sin x dx, is a fundamental concept in calculus with numerous applications in various fields like physics, engineering, and signal processing. This article will delve deep into this integral, exploring its calculation, geometrical interpretation, and practical significance. We will also cover related concepts and applications to provide a comprehensive understanding.
Calculating the Definite Integral of sin x from 0 to π
The process of calculating this integral involves finding the antiderivative of sin x and then evaluating it at the limits of integration (0 and π).
Finding the Antiderivative
The antiderivative of sin x is -cos x. This is because the derivative of -cos x is sin x. You can verify this using the basic rules of differentiation.
Evaluating the Antiderivative at the Limits of Integration
Once we have the antiderivative, we evaluate it at the upper limit (π) and subtract the result of evaluating it at the lower limit (0). This is expressed as:
∫₀^π sin x dx = [-cos x]₀^π = (-cos π) - (-cos 0)
Since cos π = -1 and cos 0 = 1, the calculation becomes:
(-(-1)) - (-1) = 1 + 1 = 2
Therefore, the definite integral of sin x from 0 to π is 2.
Geometrical Interpretation
The definite integral ∫₀^π sin x dx has a clear geometrical interpretation. It represents the area under the curve of the function y = sin x between x = 0 and x = π.
The graph of y = sin x from 0 to π forms a curve above the x-axis. The integral calculates the area of this region. Since the sine function is positive in this interval, the area is positive, which aligns with our calculated result of 2. The area is comprised of a smooth, symmetrical curve, making the calculation of this integral particularly elegant.
Imagine trying to approximate this area using rectangles or trapezoids. The more subdivisions you use, the more accurate your approximation becomes, converging towards the exact value of 2. This geometric visualization helps solidify the understanding of what the integral represents. The area calculation highlights the power of calculus in solving problems that would be difficult or impossible to solve using only geometry.
Visualizing the Area
Imagine the graph of y = sin x. From x = 0 to x = π, the curve lies entirely above the x-axis. The integral calculates the area bounded by this curve, the x-axis, and the vertical lines x = 0 and x = π. This area is a region with a smooth, undulating boundary, contrasting with the sharp-edged shapes commonly used in basic geometry problems. This highlights the advantage of integral calculus in dealing with areas of irregular shapes.
Applications of the Integral
The integral ∫₀^π sin x dx, and its related concepts, has numerous applications in various fields:
1. Physics: Calculating Work
In physics, the definite integral is often used to calculate work done by a force. If a force F(x) is applied along the x-axis, the work done in moving an object from x = a to x = b is given by:
W = ∫ₐᵇ F(x) dx
If the force is a sinusoidal function, like in some simple harmonic motion problems, the integral ∫₀^π sin x dx or its variations would be used in the calculation. Understanding this integral forms a fundamental stepping stone for understanding more complex physics phenomena.
2. Signal Processing: Fourier Analysis
Fourier analysis, a cornerstone of signal processing, utilizes trigonometric functions like sine and cosine to decompose complex signals into simpler components. The integral of sine functions over specific intervals, including the integral from 0 to π, plays a crucial role in calculating the Fourier coefficients. These coefficients help to represent the original signal as a sum of simpler sine and cosine waves, making it easier to analyze and manipulate.
3. Probability and Statistics: Probability Density Functions
In probability and statistics, the integral of a probability density function (PDF) over a specific range gives the probability that a random variable falls within that range. While the simple sine function might not be a commonly used PDF in itself, the principles of integration involved in solving this problem are directly transferable to solving more complex probability problems involving other functions.
Extending the Concept: Integrals Involving Variations of sin x
Understanding the integral of sin x from 0 to π lays the foundation for solving many related integrals. Let's explore some variations:
1. Integrals Over Different Intervals
The integral of sin x can be calculated over different intervals. For example, ∫₀²π sin x dx = 0, because the positive area from 0 to π is canceled out by the negative area from π to 2π. This demonstrates the importance of considering the interval of integration when evaluating a definite integral.
2. Integrals with Multiplicative Constants
If we have an integral of the form ∫₀^π k sin x dx, where k is a constant, the solution is simply k times the integral of sin x from 0 to π, resulting in 2k. This showcases the linearity property of definite integrals.
3. Integrals with Added Constants
The integral of sin x + c, where c is a constant, from 0 to π, can be calculated by splitting the integral into two parts: ∫₀^π sin x dx + ∫₀^π c dx. The result is 2 + cπ. This demonstrates how to deal with integrals involving sums of functions.
Conclusion: The Significance of ∫₀^π sin x dx
The seemingly simple definite integral ∫₀^π sin x dx = 2 holds immense significance in mathematics and its applications. It's a fundamental building block in calculus, representing a crucial step in understanding more complex integration techniques and their widespread application in science and engineering. Its geometric interpretation provides intuitive understanding, while its utilization in diverse fields highlights its practical relevance. The exploration of variations and related integrals further strengthens our comprehension of this key mathematical concept and its role in various disciplines. Mastering this integral and its variations is essential for anyone pursuing advanced studies in mathematics, physics, engineering, or related fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about Integral Sin X From 0 To Pi . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.