Integration Of Cos X Sin X
News Co
Apr 11, 2025 · 5 min read
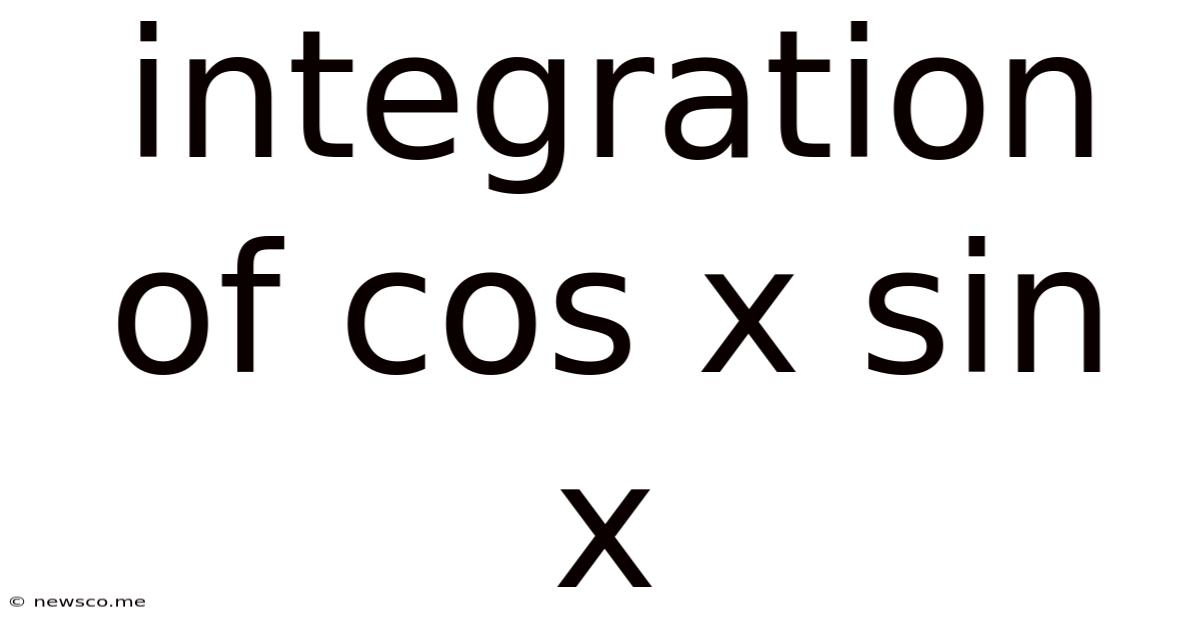
Table of Contents
The Fascinating World of Cos x Sin x Integration: Techniques and Applications
The integration of cos x sin x, seemingly a simple trigonometric expression, unveils a rich tapestry of mathematical techniques and applications. While straightforward at first glance, understanding its integration thoroughly requires a grasp of various integration methods, trigonometric identities, and their practical implications across diverse fields. This comprehensive guide will delve into the intricacies of integrating cos x sin x, exploring multiple approaches and showcasing their relevance in real-world scenarios.
Understanding the Fundamental Trigonometric Identities
Before diving into the integration process, it's crucial to refresh our understanding of fundamental trigonometric identities. These identities are the cornerstone of simplifying trigonometric expressions and making integration more manageable. Key identities relevant to our discussion include:
-
Double Angle Identities: These are pivotal in simplifying expressions involving products of sine and cosine. The most relevant here is:
- sin(2x) = 2sin(x)cos(x) This identity directly relates the product cos(x)sin(x) to the sine of double the angle.
-
Power-Reducing Formulas: While not directly needed for the simplest case, these are essential when dealing with higher powers of sine and cosine. These formulas express powers of sine and cosine in terms of lower powers, often making integration significantly easier.
Method 1: Utilizing the Double Angle Identity
The most straightforward and efficient method for integrating cos(x)sin(x) is leveraging the double angle identity. By rewriting the expression using this identity, we transform a product of trigonometric functions into a single trigonometric function, simplifying the integration process considerably.
Step 1: Apply the Double Angle Identity
We begin by recognizing that cos(x)sin(x) can be rewritten as (1/2)sin(2x) using the double angle formula.
Step 2: Integrate the Simplified Expression
Integrating (1/2)sin(2x) is now a straightforward task:
∫cos(x)sin(x) dx = ∫(1/2)sin(2x) dx = -(1/4)cos(2x) + C
where C represents the constant of integration.
This method elegantly solves the integral using a simple substitution and a well-known integral. Its simplicity and efficiency make it the preferred method for most cases.
Practical Applications of this Method
This integration technique finds applications in various fields, including:
-
Physics: In oscillatory systems like simple harmonic motion, the solutions often involve sine and cosine functions. This integration method is crucial for calculating displacement, velocity, and acceleration.
-
Electrical Engineering: Analyzing alternating current (AC) circuits necessitates dealing with sinusoidal waveforms. This integration helps in determining parameters such as power and energy in such circuits.
-
Signal Processing: Signal processing relies heavily on Fourier analysis, which involves decomposing signals into sinusoidal components. The integration of expressions like cos(x)sin(x) becomes essential in various signal processing algorithms.
Method 2: Integration by Parts
While the double angle method is the most efficient, understanding alternative approaches broadens mathematical perspectives. Integration by parts provides another, albeit more complex, route to solving this integral.
Step 1: Choose u and dv
Let's choose:
- u = cos(x) => du = -sin(x)dx
- dv = sin(x)dx => v = -cos(x)
Step 2: Apply the Integration by Parts Formula
The integration by parts formula states: ∫u dv = uv - ∫v du
Applying this formula, we get:
∫cos(x)sin(x)dx = -cos(x)cos(x) - ∫(-cos(x))(-sin(x))dx
This simplifies to:
∫cos(x)sin(x)dx = -cos²(x) - ∫cos(x)sin(x)dx
Step 3: Solve for the Integral
Notice that the original integral appears on both sides of the equation. We can solve for it:
2∫cos(x)sin(x)dx = -cos²(x)
∫cos(x)sin(x)dx = -(1/2)cos²(x) + C
Step 4: Reconciling the Result
This result looks different from the one obtained using the double angle formula. However, using trigonometric identities, we can show that these two results are equivalent, differing only by a constant of integration. This demonstrates the flexibility of integration techniques.
Limitations of Integration by Parts in this Case
While integration by parts works, it's significantly less efficient than the double angle method. The double angle method provides a more direct and concise solution. Integration by parts introduces an extra step that's unnecessary in this particular scenario.
Method 3: Substitution Method
Another approach, though not as elegant as the double angle method, involves using a substitution.
Step 1: Choose a Substitution
Let u = sin(x). Then du = cos(x)dx.
Step 2: Rewrite the Integral
The integral becomes:
∫u du
Step 3: Integrate and Substitute Back
∫u du = (1/2)u² + C = (1/2)sin²(x) + C
Step 4: Reconciliation
Again, this result appears different from the previous ones but can be shown equivalent using trigonometric identities and adjusting the constant of integration.
Integrating Higher Powers of Cos x and Sin x
The methods described above primarily focus on the simplest case of cos(x)sin(x). However, scenarios involving higher powers of cos(x) and sin(x), such as cos²(x)sin(x) or cos³(x)sin²(x), require more advanced techniques. These often involve:
-
Power-reducing formulas: These formulas express higher powers of sine and cosine in terms of lower powers, making integration more tractable. For example, cos²(x) = (1+cos(2x))/2.
-
Multiple angle formulas: These help express products of trigonometric functions as sums or differences, simplifying the integration.
-
Recursive formulas: In some cases, recursive formulas can be derived to systematically reduce the powers of sine and cosine.
Conclusion: A Versatile Integral with Wide Applications
The integration of cos(x)sin(x), while seemingly simple, highlights the power and versatility of various integration techniques. The double angle method emerges as the most efficient and straightforward approach, but understanding alternative methods like integration by parts and substitution expands mathematical proficiency. The applications of this integral extend across multiple disciplines, demonstrating its significance in solving real-world problems. Mastering the integration of cos(x)sin(x) and understanding its variations lays a crucial foundation for tackling more complex trigonometric integrals and their applications in diverse fields. Further exploration of power-reducing formulas and other advanced techniques will equip you to handle the complexities of higher-power trigonometric integrals. Remember to always check your solutions using different methods to build confidence and solidify your understanding. The world of trigonometric integration is vast, and each solved integral is a step towards a deeper appreciation of mathematics and its power.
Latest Posts
Related Post
Thank you for visiting our website which covers about Integration Of Cos X Sin X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.