Is 1/3 And 1/3 Equal 2/3
News Co
Apr 24, 2025 · 5 min read
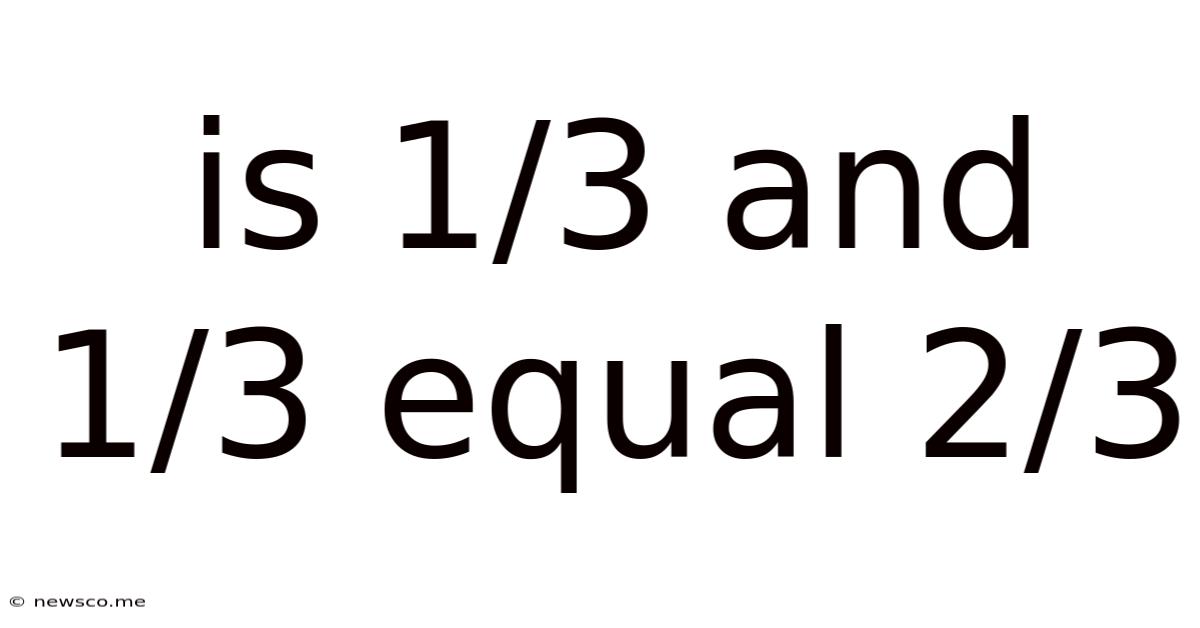
Table of Contents
Is 1/3 + 1/3 Equal to 2/3? A Deep Dive into Fraction Addition
The seemingly simple question, "Is 1/3 + 1/3 equal to 2/3?" might seem trivial at first glance. However, a deeper exploration reveals crucial concepts in mathematics, particularly in the realm of fractions, and offers valuable insights for students and educators alike. This article will delve into not only the answer but also the underlying principles, providing a comprehensive understanding of fraction addition and its applications.
Understanding Fractions: The Building Blocks
Before tackling the addition problem, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 1/3, the numerator (1) represents one part, and the denominator (3) indicates that the whole is divided into three equal parts. Understanding this fundamental concept is critical for mastering fraction addition and other fraction operations.
Adding Fractions: A Step-by-Step Guide
Adding fractions, particularly those with the same denominator (like our 1/3 + 1/3 example), is a straightforward process:
-
Check the Denominators: Ensure both fractions have the same denominator. If they do, proceed to the next step. If not, you'll need to find a common denominator before adding. We'll explore this in more detail later.
-
Add the Numerators: Add the numerators of the fractions while keeping the denominator the same.
-
Simplify (if necessary): After adding, simplify the resulting fraction to its lowest terms. This involves dividing both the numerator and the denominator by their greatest common divisor (GCD).
Let's apply this to our problem: 1/3 + 1/3
-
Denominators are the same: Both fractions have a denominator of 3.
-
Add the numerators: 1 + 1 = 2
-
Result: The sum is 2/3. This fraction is already in its simplest form.
Therefore, yes, 1/3 + 1/3 = 2/3.
Visual Representation: Understanding with Pictures
Visual aids are invaluable for grasping mathematical concepts. Let's visualize 1/3 + 1/3 using a simple diagram:
Imagine a circle divided into three equal parts. Shading one part represents 1/3. Shading another part represents another 1/3. Together, the shaded parts represent 2/3 of the circle. This visual representation provides a concrete understanding of the addition process.
Adding Fractions with Different Denominators: A More Complex Scenario
The process becomes slightly more complex when adding fractions with different denominators. In such cases, finding a common denominator is the crucial first step. A common denominator is a number that is divisible by both denominators. The least common denominator (LCD) is the smallest such number, making simplification easier.
Example: Let's add 1/2 + 1/4
-
Find the LCD: The LCD of 2 and 4 is 4.
-
Convert to equivalent fractions: Rewrite each fraction with the LCD as the denominator. 1/2 becomes 2/4 (multiplying the numerator and denominator by 2).
-
Add the numerators: 2/4 + 1/4 = 3/4
-
Simplify (if necessary): 3/4 is already in its simplest form.
Therefore, 1/2 + 1/4 = 3/4
Real-World Applications of Fraction Addition
Fraction addition isn't just a theoretical concept; it finds numerous practical applications in everyday life:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. Adding fractions is essential for accurate measurements.
-
Construction and Engineering: Precise measurements are vital in construction and engineering. Fraction addition helps in calculating distances, areas, and volumes.
-
Finance: Calculating portions of budgets, debts, or investments often involves fraction addition.
-
Data Analysis: Representing and manipulating data frequently involves fractions, and addition is a crucial tool for analysis.
Misconceptions and Common Errors
Despite the apparent simplicity, some common misconceptions can lead to errors in fraction addition:
-
Adding numerators and denominators directly: A common mistake is to simply add the numerators and the denominators, leading to incorrect results (e.g., incorrectly calculating 1/3 + 1/3 as 2/6).
-
Ignoring simplification: Failing to simplify the resulting fraction to its lowest terms can make the result less clear and may lead to further calculation errors.
-
Incorrectly finding the LCD: Mistakes in identifying the least common denominator can lead to incorrect results.
Advanced Concepts and Extensions
The principles of fraction addition lay the foundation for more complex mathematical concepts:
-
Fraction Subtraction: Subtracting fractions follows a similar process to addition, but involves subtracting numerators instead of adding them.
-
Fraction Multiplication and Division: These operations involve different rules and concepts than addition and subtraction.
-
Algebraic Fractions: In algebra, fractions involving variables are manipulated using similar principles to those discussed here.
Conclusion: Mastering Fraction Addition for Success
Understanding fraction addition is a fundamental building block in mathematics. Mastering this skill opens doors to more advanced mathematical concepts and countless practical applications in everyday life. By thoroughly grasping the principles explained in this article, students and anyone interested in strengthening their math skills can confidently tackle fraction addition problems and avoid common errors. Remember to focus on understanding the underlying concepts, utilizing visual aids when helpful, and practicing regularly to build fluency and confidence. The seemingly simple question of "Is 1/3 + 1/3 equal to 2/3?" serves as a gateway to a deeper understanding of a crucial mathematical skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 1/3 And 1/3 Equal 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.