Is .125 The Same As 1/8
News Co
Mar 26, 2025 · 4 min read
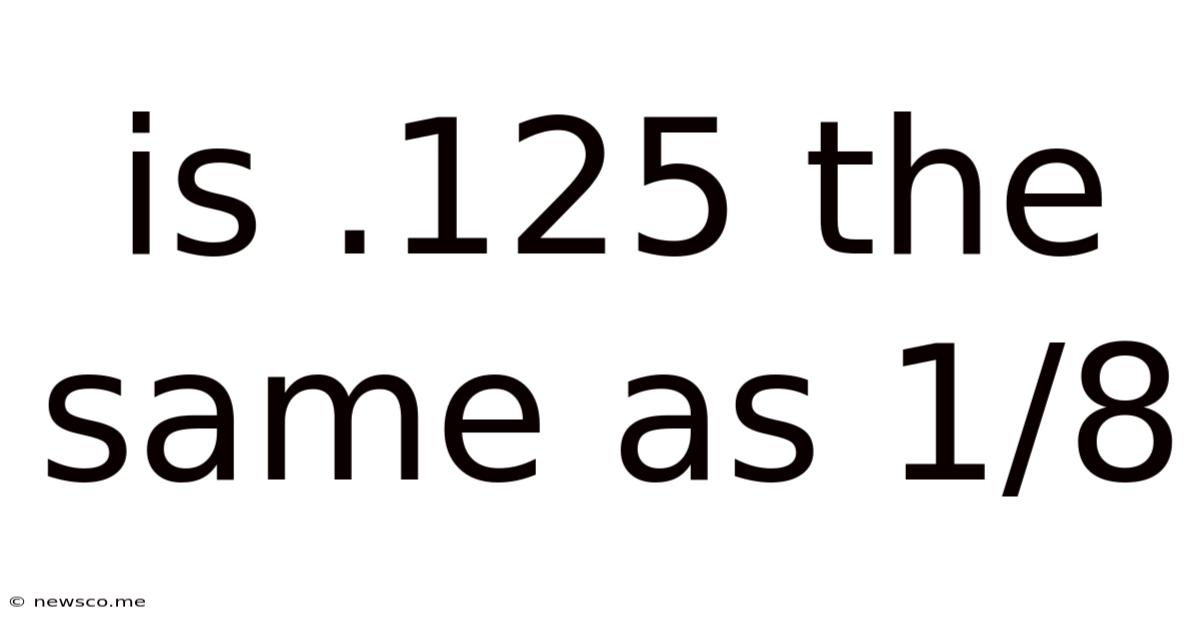
Table of Contents
Is .125 the Same as 1/8? A Deep Dive into Decimal and Fraction Equivalence
Are you puzzled by the relationship between decimals and fractions? Many find themselves questioning whether seemingly disparate numbers like 0.125 and 1/8 are actually equivalent. The answer, in short, is a resounding yes. But understanding why requires exploring the fundamental concepts of decimal and fractional representation. This comprehensive guide will delve into the intricacies of this equivalence, providing a clear and thorough explanation accessible to all.
Understanding Decimal Numbers
Decimal numbers are based on the base-10 system, meaning they use powers of 10 to represent values. Each digit to the right of the decimal point represents a fraction with a denominator that is a power of 10. For example:
- 0.1 represents 1/10 (one-tenth)
- 0.01 represents 1/100 (one-hundredth)
- 0.001 represents 1/1000 (one-thousandth)
The number 0.125 can be broken down as follows:
- 0.1 = 1/10
- 0.02 = 2/100
- 0.005 = 5/1000
Adding these fractions together: 1/10 + 2/100 + 5/1000 = 100/1000 + 20/1000 + 5/1000 = 125/1000
Understanding Fractions
Fractions represent a part of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered. For example, 1/8 means one part out of eight equal parts.
Proving the Equivalence: 0.125 = 1/8
To definitively prove that 0.125 is equal to 1/8, we can use several methods:
Method 1: Converting the Decimal to a Fraction
As shown above, we've already broken down 0.125 into the fraction 125/1000. Now, we simplify this fraction by finding the greatest common divisor (GCD) of 125 and 1000. The GCD of 125 and 1000 is 125. Dividing both the numerator and the denominator by 125, we get:
125/1000 = (125 ÷ 125) / (1000 ÷ 125) = 1/8
Therefore, 0.125 simplifies to 1/8.
Method 2: Converting the Fraction to a Decimal
Alternatively, we can convert the fraction 1/8 into a decimal by performing long division:
1 ÷ 8 = 0.125
This directly demonstrates that 1/8 is equal to 0.125.
Method 3: Using Proportions
We can also use proportions to show the equivalence. We know that 1/8 represents one part out of eight. If we multiply both the numerator and denominator by 125, we obtain:
(1 x 125) / (8 x 125) = 125/1000
As we've already established, 125/1000 is equal to 0.125.
Practical Applications and Importance
Understanding the equivalence between 0.125 and 1/8 is crucial in various fields, including:
- Mathematics: This equivalence is fundamental for simplifying calculations, solving equations, and understanding the relationship between different number systems.
- Engineering: Precise measurements and calculations often require converting between decimals and fractions for accuracy.
- Construction: Many construction projects utilize fractions and decimals interchangeably, making understanding their equivalence critical for accurate measurements and material estimations.
- Computer Science: Binary representation in computers often involves fractions and decimals, requiring programmers to understand their interrelation.
- Everyday Life: From cooking (measuring ingredients) to finance (calculating percentages), understanding the equivalence helps in practical situations.
Common Mistakes to Avoid
While the equivalence is straightforward, some common mistakes can lead to confusion:
- Incorrect Simplification: Failing to simplify fractions to their lowest terms can lead to inaccurate results and make comparisons difficult. Always ensure your fractions are simplified.
- Rounding Errors: When converting between decimals and fractions, rounding errors can occur. It’s crucial to maintain precision throughout the conversion process to avoid inaccuracies.
- Misunderstanding Place Value: A lack of understanding of place value in decimal numbers can lead to errors in converting decimals to fractions. Remember each place value represents a power of ten.
Expanding Your Understanding: Other Decimal-Fraction Equivalents
Understanding the equivalence between 0.125 and 1/8 opens the door to exploring other common decimal-fraction equivalents. For instance:
- 0.5 = 1/2
- 0.25 = 1/4
- 0.75 = 3/4
- 0.333... = 1/3 (Note the repeating decimal)
- 0.666... = 2/3 (Note the repeating decimal)
Mastering these equivalents enhances your mathematical fluency and problem-solving abilities.
Conclusion: The Power of Equivalence
The equivalence between 0.125 and 1/8 underscores the interconnectedness of decimal and fractional representations. By understanding the methods for converting between these forms and appreciating their practical applications, you can enhance your mathematical skills and navigate various quantitative challenges with greater confidence. Remember to practice regularly, paying close attention to simplification and precision to avoid common errors. The more comfortable you become with converting between decimals and fractions, the more effective you'll be in tackling numerical problems across numerous disciplines. This seemingly simple equivalence holds significant power in expanding your mathematical understanding and competence.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Is .125 The Same As 1/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.