Is 2 1/3 Equal To 2/3
News Co
Apr 21, 2025 · 5 min read
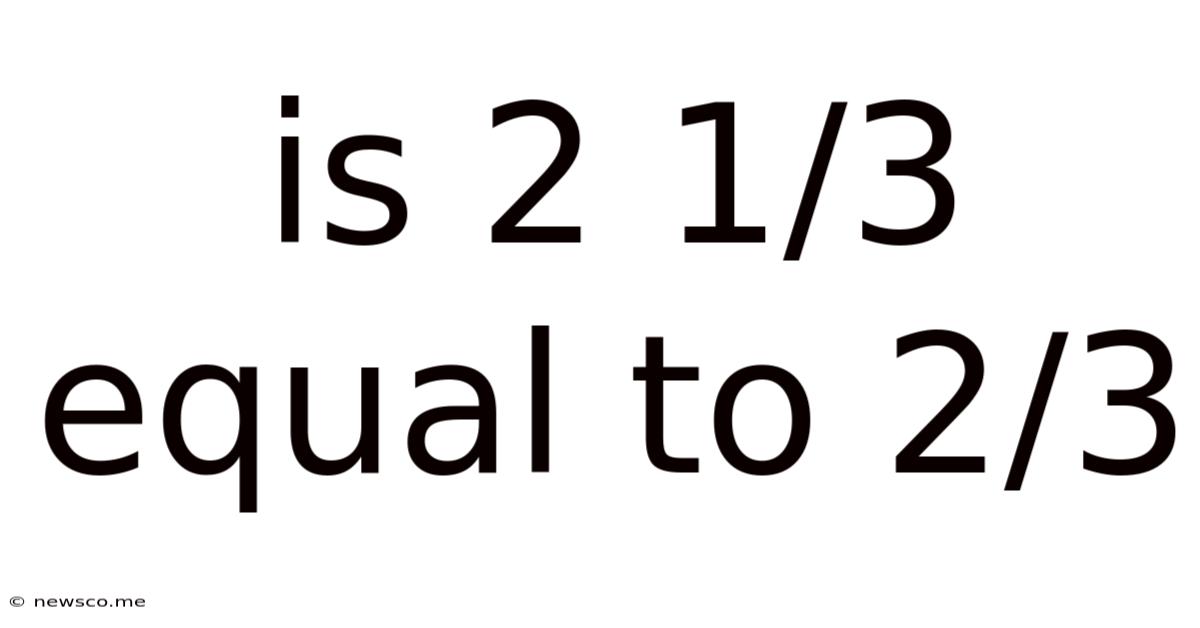
Table of Contents
Is 2 1/3 Equal to 2/3? A Deep Dive into Fraction Equivalence
The question, "Is 2 1/3 equal to 2/3?" might seem simple at first glance. However, a thorough understanding of fractions and their representation is crucial to grasping why the answer is a resounding no. This article will delve into the fundamental concepts of fractions, mixed numbers, and equivalent fractions, providing a comprehensive explanation of why 2 1/3 and 2/3 are distinctly different, and how to avoid such misconceptions.
Understanding Fractions: The Building Blocks
Before addressing the core question, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator specifies how many of those parts are being considered.
For example, in the fraction 1/4, the denominator (4) means the whole is divided into four equal parts, and the numerator (1) indicates we're considering one of those parts.
Mixed Numbers vs. Improper Fractions
Fractions come in two main forms:
-
Proper fractions: The numerator is smaller than the denominator (e.g., 1/2, 3/4, 5/8). These fractions represent a value less than 1.
-
Improper fractions: The numerator is equal to or larger than the denominator (e.g., 5/4, 7/3, 9/9). These fractions represent a value greater than or equal to 1.
-
Mixed numbers: These combine a whole number and a proper fraction (e.g., 2 1/3, 1 3/4, 5 2/5). They represent a value greater than 1. The number to the left of the space is the whole number.
Key takeaway: Understanding the difference between improper fractions and mixed numbers is essential for correctly comparing and manipulating fractions.
Converting Mixed Numbers to Improper Fractions
To effectively compare fractions, it's often beneficial to convert mixed numbers into improper fractions. This involves expressing the whole number as a fraction with the same denominator as the fractional part and then adding the two fractions.
Let's convert 2 1/3 to an improper fraction:
- Multiply the whole number by the denominator: 2 * 3 = 6
- Add the numerator: 6 + 1 = 7
- Keep the same denominator: 3
Therefore, 2 1/3 is equivalent to the improper fraction 7/3.
Comparing Fractions: Unveiling the Discrepancy
Now, let's directly compare 2 1/3 (or its improper fraction equivalent 7/3) and 2/3. It's clear that they are not equal.
- 2/3 represents two parts out of three equal parts of a whole.
- 7/3 represents seven parts out of three equal parts of a whole, which is equivalent to two whole units and one-third of a unit.
Visually, imagine a pizza cut into three slices. 2/3 represents two slices, while 7/3 represents two whole pizzas and one additional slice from a third pizza.
The difference is significant: 7/3 is considerably larger than 2/3. Their values are not interchangeable.
Equivalent Fractions: A Clarification
Equivalent fractions represent the same value but have different numerators and denominators. They are obtained by multiplying or dividing both the numerator and denominator by the same non-zero number. For example:
-
1/2 is equivalent to 2/4, 3/6, 4/8, and so on (multiplying both numerator and denominator by the same number).
-
6/9 is equivalent to 2/3 (dividing both numerator and denominator by 3).
It's important to note that finding equivalent fractions does not change the underlying value of the fraction. While 2/3 is equivalent to 4/6, it is not equivalent to 7/3. There's no way to obtain 7/3 from 2/3 through multiplication or division of both the numerator and denominator by the same number.
Avoiding Common Mistakes
Many misconceptions about fractions arise from a lack of understanding of their fundamental principles. Here are some common pitfalls to avoid:
-
Confusing numerators and denominators: Always remember that the denominator represents the total number of parts, and the numerator represents the number of parts considered.
-
Incorrectly adding or subtracting fractions: Fractions must have a common denominator before they can be added or subtracted.
-
Ignoring whole numbers in mixed numbers: When converting mixed numbers, remember to incorporate the whole number into the improper fraction conversion.
-
Assuming all fractions with the same denominator are equivalent: Fractions with the same denominator might not represent the same value.
The Importance of Mastering Fractions
A solid understanding of fractions is fundamental to success in mathematics and many related fields. From basic arithmetic to advanced calculus, fractions are ubiquitous. A firm grasp of fraction equivalence, conversion between mixed numbers and improper fractions, and the ability to compare and manipulate fractions is essential for problem-solving and critical thinking.
Real-World Applications of Fraction Understanding
Understanding fractions isn't just confined to the classroom. It has numerous real-world applications:
-
Cooking and Baking: Recipes often use fractions for precise measurements of ingredients. Incorrectly interpreting fractions can lead to disastrous culinary results!
-
Construction and Engineering: Accurate measurements and calculations are crucial, and fractions are frequently used in blueprints and designs.
-
Finance: Understanding fractions is essential for calculating percentages, interest rates, and other financial metrics.
-
Data Analysis: Many statistical analyses involve working with fractions and proportions.
-
Everyday Life: Dividing resources, sharing tasks, and understanding proportions all rely on a fundamental understanding of fractions.
Conclusion: 2 1/3 and 2/3 are Distinctly Different
To reiterate, 2 1/3 is not equal to 2/3. They represent entirely different values. 2 1/3 is equivalent to 7/3, which is significantly larger than 2/3. By understanding the fundamental concepts of fractions, mixed numbers, improper fractions, and equivalent fractions, we can confidently differentiate between these values and avoid common errors in calculations and interpretations. Mastering fractions is a crucial skill that empowers us to confidently navigate various mathematical and real-world challenges. The seemingly simple question of comparing 2 1/3 and 2/3 highlights the importance of a thorough understanding of these foundational concepts. Remember the difference and continue to build your understanding of this essential mathematical tool!
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 2 1/3 Equal To 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.