Is 2 3 4 Bigger Than 2 5 8
News Co
Apr 02, 2025 · 5 min read
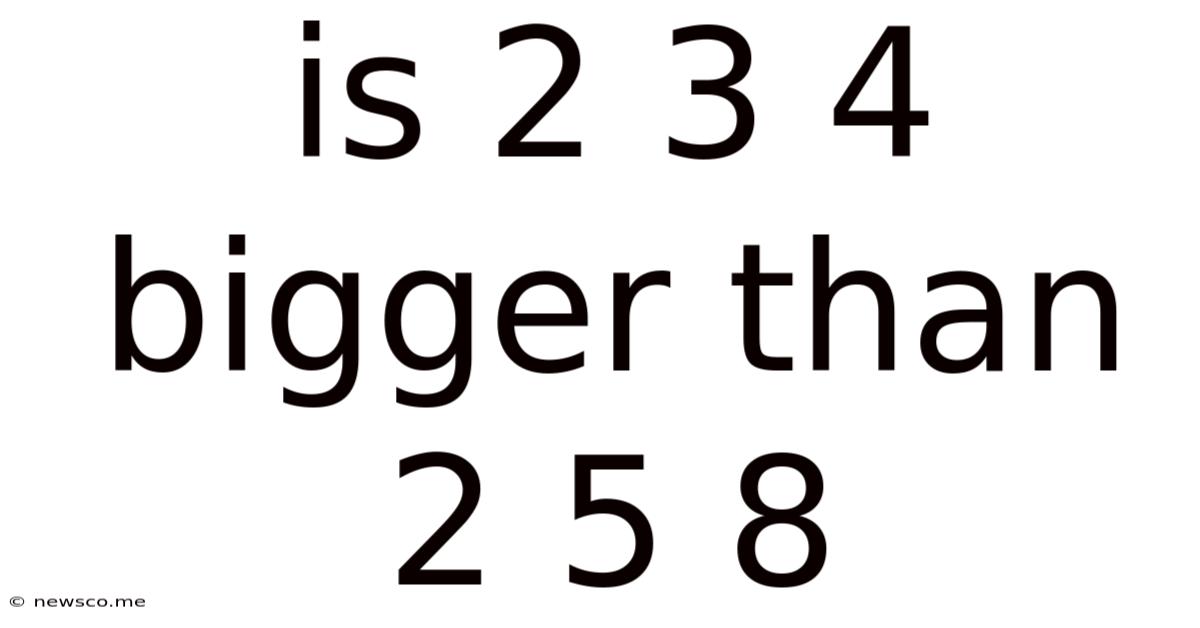
Table of Contents
Is 2 3 4 Bigger Than 2 5 8? A Deep Dive into Comparing Numbers
The seemingly simple question, "Is 2 3 4 bigger than 2 5 8?" might seem trivial at first glance. However, a nuanced exploration reveals deeper concepts about number systems, place value, and the importance of context in numerical comparisons. This article will delve into the various interpretations and considerations necessary to answer this question definitively and explore related mathematical principles.
Understanding the Context: The Role of Number Systems
The initial difficulty lies in the lack of explicit information about the number system being used. Are these decimal numbers (base 10), binary numbers (base 2), hexadecimal numbers (base 16), or something else entirely? The answer dramatically changes depending on the base.
1. Decimal Number System (Base 10):
In the most common number system, the decimal system (base 10), the numbers are interpreted as:
- 2 3 4 represents two hundred and thirty-four (200 + 30 + 4).
- 2 5 8 represents two hundred and fifty-eight (200 + 50 + 8).
Therefore, in the decimal system, 258 is clearly bigger than 234.
2. Other Number Systems:
If we consider other number systems, the interpretation and comparison differ significantly:
-
Binary (Base 2): If "2 3 4" and "2 5 8" represent binary numbers, this notation is unconventional. Binary numbers typically only use 0 and 1. If we assume these are concatenated sequences, we'd need clarification on how to interpret the spaces.
-
Hexadecimal (Base 16): Similar to binary, if we assume these are hexadecimal numbers, the use of digits beyond 9 (like 2, 3, 4, 5, 8) is valid, but we again need a clearer interpretation of the spaces. In a standard hexadecimal notation, 234<sub>16</sub> and 258<sub>16</sub> would be valid numbers, and their decimal equivalents could be compared. However, that would require converting them into their decimal counterparts first.
-
Other Bases: The same principle applies to other bases. Without knowing the base, any comparison is speculative.
The Importance of Place Value
The fundamental concept underpinning our ability to compare numbers, particularly in the decimal system, is place value. Each digit in a number holds a specific value determined by its position. In the decimal system, the rightmost digit represents the ones place, the next digit to the left represents the tens place, the next the hundreds place, and so on. This system allows us to represent large numbers efficiently.
For example, in 234:
- 4 is in the ones place (4 x 10<sup>0</sup> = 4)
- 3 is in the tens place (3 x 10<sup>1</sup> = 30)
- 2 is in the hundreds place (2 x 10<sup>2</sup> = 200)
The sum of these values (4 + 30 + 200) gives us 234. This same principle applies to 258, demonstrating that the number with a higher value in the tens or hundreds place will inherently be larger.
Addressing Potential Ambiguities and Misinterpretations
The original question's ambiguity highlights the importance of clear and unambiguous notation in mathematics. To avoid confusion, it is crucial to:
- Specify the number system: Explicitly state whether the numbers are decimal, binary, hexadecimal, or another base.
- Use appropriate separators: If the numbers are not single digits, use clear separators like commas or periods to avoid misinterpretations (e.g., 2,34 or 2.34).
- Contextualize the numbers: Explain the units or quantities being represented by these numbers. Are these measurements, counts, indices, or something else?
Beyond Simple Comparisons: Exploring Mathematical Operations
Once the number system is clarified, comparing 234 and 258 involves a simple subtraction: 258 - 234 = 24. This difference confirms that 258 is 24 units greater than 234. This seemingly simple subtraction highlights the power of basic mathematical operations in solving even seemingly trivial questions.
Expanding the Scope: Advanced Mathematical Concepts
While the initial comparison might seem elementary, it opens doors to exploring more advanced mathematical concepts:
-
Inequalities: The comparison can be represented formally using inequalities: 234 < 258 (234 is less than 258) or 258 > 234 (258 is greater than 234).
-
Number Line Visualization: A number line can visually represent the relative positions of 234 and 258, clearly showing that 258 is further to the right (and thus larger).
-
Order of Operations (PEMDAS/BODMAS): While not directly applicable to this specific comparison, understanding the order of operations is crucial when dealing with more complex mathematical expressions.
-
Set Theory: In set theory, we could consider these numbers as elements of a set of natural numbers, and their comparison would involve determining the order within that set.
-
Number Theory: Various number theory concepts, like divisibility, prime factorization, and modular arithmetic, could be applied if we extended the scope beyond simple comparisons.
Conclusion: The Importance of Precision and Clarity
The seemingly simple question of whether 2 3 4 is bigger than 2 5 8 emphasizes the importance of precision, clarity, and understanding fundamental mathematical principles. The context, specifically the number system employed, significantly impacts the answer. In the commonly understood decimal system, 258 is unequivocally larger than 234. However, this elementary example serves as a valuable reminder of the need for precise notation and careful consideration of context when dealing with numerical comparisons, regardless of their apparent simplicity. The exploration goes beyond a simple answer, revealing the underlying principles of place value, different number systems, and the importance of unambiguous mathematical expression. This simple problem becomes a gateway to understanding more complex mathematical concepts and the critical role of precision in any mathematical discussion.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 2 3 4 Bigger Than 2 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.