Is 2 3 Equal To 8 12
News Co
Mar 18, 2025 · 5 min read
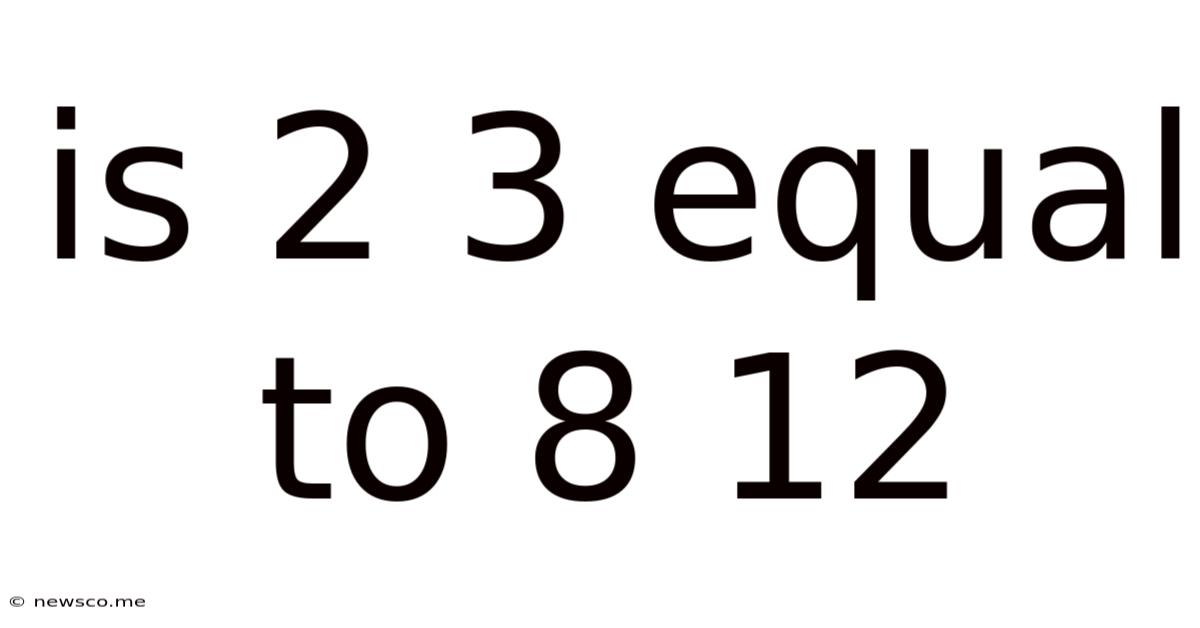
Table of Contents
Is 2/3 Equal to 8/12? A Deep Dive into Fraction Equivalence
The question, "Is 2/3 equal to 8/12?" might seem simple at first glance, especially for those well-versed in mathematics. However, understanding the underlying principles of fraction equivalence is crucial for a solid grasp of mathematical concepts and problem-solving. This article will delve into the intricacies of this seemingly straightforward question, exploring the concepts of equivalent fractions, simplifying fractions, and the broader implications of understanding fractional relationships.
Understanding Fractions: The Building Blocks
Before diving into the equivalence of 2/3 and 8/12, let's establish a firm understanding of what fractions represent. A fraction is a numerical representation of a part of a whole. It consists of two main components:
- Numerator: The top number, representing the number of parts considered.
- Denominator: The bottom number, representing the total number of equal parts that make up the whole.
For example, in the fraction 2/3, the numerator (2) indicates we are considering two parts, while the denominator (3) signifies that the whole is divided into three equal parts.
Equivalent Fractions: The Concept of Equality
Equivalent fractions represent the same proportion or value, even though they look different. They are essentially different ways of expressing the same part of a whole. The key to identifying equivalent fractions lies in the concept of multiplying or dividing both the numerator and the denominator by the same non-zero number. This process doesn't change the overall value of the fraction; it simply changes its representation.
Visualizing Equivalence
Imagine a pizza cut into three equal slices. If you take two of those slices, you have 2/3 of the pizza. Now, imagine the same pizza, but this time it's cut into twelve equal slices. If you take eight of these slices, you still have the same amount of pizza – two-thirds. This visual representation demonstrates that 2/3 and 8/12 are equivalent fractions.
Simplifying Fractions: Finding the Simplest Form
Simplifying a fraction involves reducing it to its lowest terms, meaning both the numerator and the denominator have no common factors other than 1. This process is essential for clarity and ease of comparison. To simplify a fraction, we divide both the numerator and the denominator by their greatest common divisor (GCD).
Let's take the fraction 8/12. The GCD of 8 and 12 is 4. Dividing both the numerator and the denominator by 4, we get:
8 ÷ 4 = 2 12 ÷ 4 = 3
Therefore, the simplified form of 8/12 is 2/3. This confirms that 2/3 and 8/12 are indeed equivalent fractions.
The Mathematical Proof: Why 2/3 = 8/12
The equivalence of 2/3 and 8/12 can be mathematically proven using the principle of multiplying both the numerator and the denominator by the same number. In this case, we can multiply the numerator and denominator of 2/3 by 4:
(2 × 4) / (3 × 4) = 8/12
This demonstrates that multiplying 2/3 by 4/4 (which is equal to 1, and multiplying by 1 doesn't change the value) results in the fraction 8/12. This confirms their equivalence. Conversely, we can also simplify 8/12 by dividing both the numerator and the denominator by their greatest common divisor (4), which leads us back to 2/3.
Real-World Applications of Fraction Equivalence
Understanding equivalent fractions isn't just an academic exercise; it has numerous practical applications in daily life:
- Cooking and Baking: Recipes often require adjusting ingredient quantities. Knowing how to work with equivalent fractions is essential for accurate scaling.
- Construction and Engineering: Precise measurements are crucial in these fields. Equivalent fractions help ensure accuracy in calculations involving dimensions and materials.
- Finance and Budgeting: Understanding proportions and fractions is vital for managing personal finances, calculating percentages, and interpreting financial data.
- Data Analysis: In many fields, data is often represented using fractions and percentages. Understanding equivalent fractions allows for easier interpretation and comparison of data.
Beyond the Basics: Extending the Concept
The concept of equivalent fractions extends beyond simple numerical examples. It lays the foundation for more advanced mathematical concepts, including:
- Ratios and Proportions: Equivalent fractions are fundamentally related to ratios and proportions, which are crucial in various areas like scaling maps, mixing solutions, and understanding relative quantities.
- Algebraic Equations: Solving algebraic equations often involves working with fractions and understanding their equivalence.
- Calculus: Concepts like limits and derivatives rely on a deep understanding of fractions and their behavior.
Common Mistakes to Avoid
While the concept of equivalent fractions seems straightforward, some common mistakes can lead to inaccurate calculations:
- Incorrect simplification: Dividing only the numerator or denominator by a common factor will alter the fraction's value. Both must be divided by the same number.
- Improper multiplication: Multiplying only the numerator or denominator by a number will also change the fraction's value. Both must be multiplied by the same number.
- Misunderstanding GCD: Incorrectly determining the greatest common divisor can lead to incomplete simplification.
Conclusion: Mastering Fraction Equivalence
The question, "Is 2/3 equal to 8/12?" serves as a gateway to understanding a fundamental concept in mathematics: fraction equivalence. While the answer is a resounding "yes," the underlying principles extend far beyond this simple example. Mastering this concept is not only crucial for academic success but also for navigating various aspects of daily life, from cooking to finance and beyond. By understanding the principles of simplification, multiplication, and the visual representation of fractions, one can confidently tackle more complex mathematical problems and appreciate the interconnectedness of mathematical concepts. The ability to recognize and work with equivalent fractions is a cornerstone of mathematical literacy, empowering individuals to approach numerical challenges with precision and understanding.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Is 2 3 Equal To 8 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.