Is 2 5 Greater Than 3 4
News Co
May 08, 2025 · 5 min read
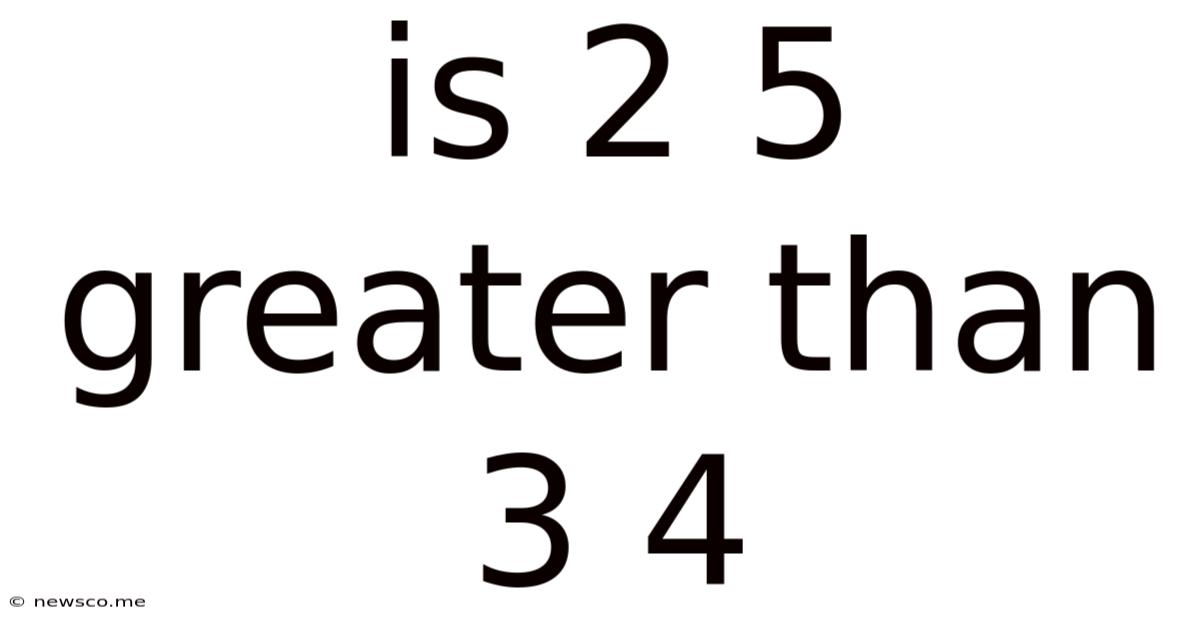
Table of Contents
Is 2/5 Greater Than 3/4? A Deep Dive into Fraction Comparison
Comparing fractions might seem like a simple task, especially when dealing with seemingly straightforward numbers like 2/5 and 3/4. However, a thorough understanding of fraction comparison techniques is crucial for various mathematical applications, from basic arithmetic to advanced calculus. This article will delve into the intricacies of comparing 2/5 and 3/4, exploring multiple methods to arrive at a definitive answer and reinforcing the underlying concepts. We'll not only determine which fraction is larger but also equip you with the skills to compare any two fractions confidently.
Understanding Fractions: A Quick Recap
Before we jump into comparing 2/5 and 3/4, let's briefly refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 2/5, 2 is the numerator (we have 2 parts), and 5 is the denominator (the whole is divided into 5 equal parts).
Method 1: Finding a Common Denominator
This is perhaps the most common and straightforward method for comparing fractions. The principle is to convert both fractions into equivalent fractions with the same denominator. This allows for a direct comparison of the numerators.
Steps:
-
Find the Least Common Multiple (LCM): Determine the least common multiple of the denominators (5 and 4). The LCM of 5 and 4 is 20.
-
Convert the Fractions: Convert each fraction to an equivalent fraction with a denominator of 20:
- 2/5 = (2 x 4) / (5 x 4) = 8/20
- 3/4 = (3 x 5) / (4 x 5) = 15/20
-
Compare the Numerators: Now that both fractions have the same denominator, we can compare their numerators directly. Since 8 < 15, we conclude that 8/20 < 15/20.
-
Conclusion: Therefore, 2/5 < 3/4. 3/4 is greater than 2/5.
Method 2: Converting to Decimals
Another effective method involves converting both fractions into their decimal equivalents. This allows for a simple numerical comparison.
Steps:
-
Divide the Numerator by the Denominator: For each fraction, divide the numerator by the denominator:
- 2/5 = 2 ÷ 5 = 0.4
- 3/4 = 3 ÷ 4 = 0.75
-
Compare the Decimal Values: Now compare the decimal values directly. Since 0.4 < 0.75, we conclude that 2/5 < 3/4.
-
Conclusion: Again, we find that 3/4 is greater than 2/5.
Method 3: Visual Representation
While not as precise as the previous methods, visualizing the fractions can provide a helpful intuitive understanding. Imagine two identical pies:
- Pie 1: Divide this pie into 5 equal slices. Shade 2 slices. This represents 2/5.
- Pie 2: Divide this pie into 4 equal slices. Shade 3 slices. This represents 3/4.
By visually comparing the shaded areas, it's apparent that the shaded portion in Pie 2 (3/4) is larger than the shaded portion in Pie 1 (2/5). This visual representation confirms that 3/4 is greater than 2/5.
Method 4: Cross-Multiplication
This method is particularly useful when comparing fractions without needing to find a common denominator.
Steps:
-
Cross-Multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice-versa:
- 2/5 and 3/4 => (2 x 4) and (3 x 5) => 8 and 15
-
Compare the Products: Compare the two products. Since 8 < 15, the fraction with the smaller product (2/5) is the smaller fraction.
-
Conclusion: This confirms that 3/4 is greater than 2/5.
Beyond the Comparison: Understanding Fraction Magnitude
Comparing 2/5 and 3/4 is not just about finding the larger fraction; it's about understanding the relative magnitudes of fractions. This understanding is crucial for problem-solving in various contexts.
Consider scenarios where this comparison might be relevant:
- Baking: If a recipe calls for 3/4 cup of sugar and you only have 2/5 of a cup, you'll be short of the required amount.
- Construction: If you need 3/4 of a meter of wood and you only have 2/5 of a meter, you'll need to acquire more.
- Data Analysis: When interpreting proportions or percentages represented as fractions, accurate comparison is essential for data interpretation.
These real-world examples highlight the practical application of understanding fraction magnitude.
Expanding Your Fraction Skills
The methods discussed above provide a strong foundation for comparing fractions. However, to further enhance your mathematical proficiency, consider exploring additional concepts:
- Improper Fractions and Mixed Numbers: Learn to convert between improper fractions (where the numerator is greater than or equal to the denominator) and mixed numbers (a whole number and a fraction).
- Simplifying Fractions: Practice simplifying fractions to their lowest terms, making comparisons easier and clearer.
- Fraction Operations: Master adding, subtracting, multiplying, and dividing fractions. This will greatly enhance your ability to work with fractions in diverse mathematical problems.
- Proportions and Ratios: Understanding proportions and ratios builds directly upon the concepts of fraction comparison and manipulation.
Conclusion: Mastering Fraction Comparison
Comparing fractions, even seemingly simple ones like 2/5 and 3/4, requires a solid understanding of fundamental mathematical principles. Whether you use the common denominator method, decimal conversion, visual representation, or cross-multiplication, the crucial point is to develop a consistent and reliable approach. The ability to confidently compare fractions is a cornerstone of mathematical literacy, paving the way for success in more complex mathematical endeavors. Remember, consistent practice is key to mastering these skills and applying them effectively in various real-world situations. So, keep practicing, and you'll become a fraction comparison expert in no time!
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 2 5 Greater Than 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.