Is 25 A Multiple Of 5
News Co
Apr 14, 2025 · 5 min read
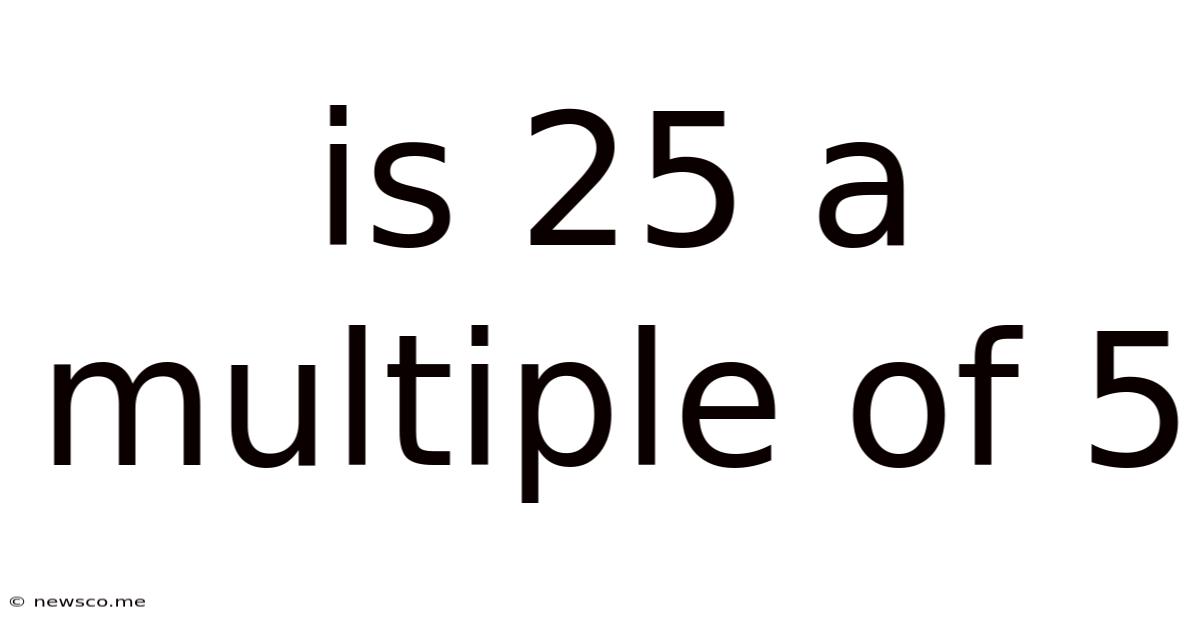
Table of Contents
Is 25 a Multiple of 5? A Deep Dive into Divisibility and Factors
The question, "Is 25 a multiple of 5?" seems deceptively simple. A quick glance might lead to an immediate "yes," but let's delve deeper into the mathematical concepts underlying this seemingly straightforward query. Understanding this will not only answer the question definitively but also illuminate the broader principles of divisibility, factors, and multiples – essential concepts in arithmetic and beyond.
Understanding Multiples
Before we tackle the specific question, let's establish a clear understanding of what constitutes a multiple. In mathematics, a multiple of a number is the product of that number and any integer (whole number). For instance:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 25, ... and so on to infinity.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30,... extending infinitely.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50... again, an infinite sequence.
Notice that multiples of any given number form an infinite sequence because you can always multiply that number by a larger and larger integer.
Understanding Factors
Closely related to multiples are factors. Factors are numbers that divide evenly into a given number without leaving a remainder. For example:
- Factors of 12: 1, 2, 3, 4, 6, and 12. Each of these numbers divides evenly into 12.
- Factors of 25: 1, 5, and 25.
Understanding factors is crucial because they help us determine whether one number is a multiple of another. If a number is a factor of another, then the second number is a multiple of the first.
The Divisibility Rule for 5
A crucial shortcut in determining multiples of 5 is the divisibility rule for 5. This rule states that a number is divisible by 5 if its last digit is either 0 or 5. Let's test this rule with some examples:
- 10: The last digit is 0, so 10 is divisible by 5 (10/5 = 2).
- 25: The last digit is 5, so 25 is divisible by 5 (25/5 = 5).
- 105: The last digit is 5, so 105 is divisible by 5 (105/5 = 21).
- 120: The last digit is 0, so 120 is divisible by 5 (120/5 = 24).
- 378: The last digit is 8, so 378 is not divisible by 5.
This rule is extremely helpful in quickly assessing divisibility without needing to perform long division.
Applying the Concepts to 25
Now, let's return to our original question: Is 25 a multiple of 5?
Using the definition of a multiple, we ask: Can 25 be expressed as the product of 5 and an integer? Yes, it can!
25 = 5 x 5
Since 5 is an integer, 25 is indeed a multiple of 5.
Alternatively, we can use the divisibility rule for 5. The last digit of 25 is 5, therefore, 25 is divisible by 5. This confirms that 25 is a multiple of 5.
Furthermore, 5 is a factor of 25, reinforcing the relationship between factors and multiples.
Beyond the Simple Answer: Exploring Deeper Mathematical Concepts
While the answer "yes" is straightforward, exploring this simple question opens doors to more complex mathematical ideas. Let's examine some related concepts:
Prime Factorization
Every whole number greater than 1 can be expressed as a product of prime numbers (numbers divisible only by 1 and themselves). This is known as prime factorization. The prime factorization of 25 is 5 x 5, or 5². This clearly demonstrates that 5 is a fundamental building block of 25.
Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
When working with multiple numbers, we often need to find their greatest common divisor (GCD) – the largest number that divides both without a remainder – and their least common multiple (LCM) – the smallest number that is a multiple of both. Understanding multiples is crucial for finding the LCM.
For instance, let's consider the numbers 25 and 15:
- Factors of 25: 1, 5, 25
- Factors of 15: 1, 3, 5, 15
The GCD of 25 and 15 is 5.
To find the LCM, we can list multiples of each number until we find a common one:
- Multiples of 25: 25, 50, 75, 100...
- Multiples of 15: 15, 30, 45, 60, 75, 90...
The LCM of 25 and 15 is 75.
Modular Arithmetic
Modular arithmetic deals with remainders after division. The expression "25 ≡ 0 (mod 5)" means that 25 leaves a remainder of 0 when divided by 5. This notation formally expresses the fact that 25 is a multiple of 5. Modular arithmetic has widespread applications in cryptography and computer science.
Real-World Applications of Multiples and Divisibility
The seemingly simple concept of multiples has far-reaching applications in various fields:
- Measurement and Conversion: Converting units of measurement often involves using multiples. For example, converting inches to feet (12 inches = 1 foot) relies on the understanding of multiples.
- Scheduling and Time Management: Understanding multiples is essential for scheduling recurring events, such as meetings or appointments that occur every 5 days or weeks.
- Pattern Recognition: Many natural and man-made patterns involve repeating sequences, which are inherently related to multiples.
- Computer Science and Programming: Multiples are fundamental in many algorithms and data structures used in computer programming.
- Engineering and Design: Divisibility and multiples are crucial in designing structures and systems that need to be divided into equal parts.
Conclusion: The Significance of a Simple Question
The seemingly trivial question, "Is 25 a multiple of 5?" serves as a gateway to explore fundamental mathematical concepts with wide-ranging applications. By understanding multiples, factors, divisibility rules, prime factorization, and related concepts, we gain a deeper appreciation for the structure and elegance of mathematics and its importance in our daily lives. The answer, "yes," is not merely a factual statement but a starting point for a rich exploration of mathematical principles. This simple question reinforces the power of foundational mathematical knowledge and its pervasive influence on various aspects of our world. The ability to quickly and accurately determine multiples is a valuable skill that extends far beyond the classroom and into numerous practical situations.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 25 A Multiple Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.