Is 25 Square Root A Rational Number
News Co
Apr 16, 2025 · 5 min read
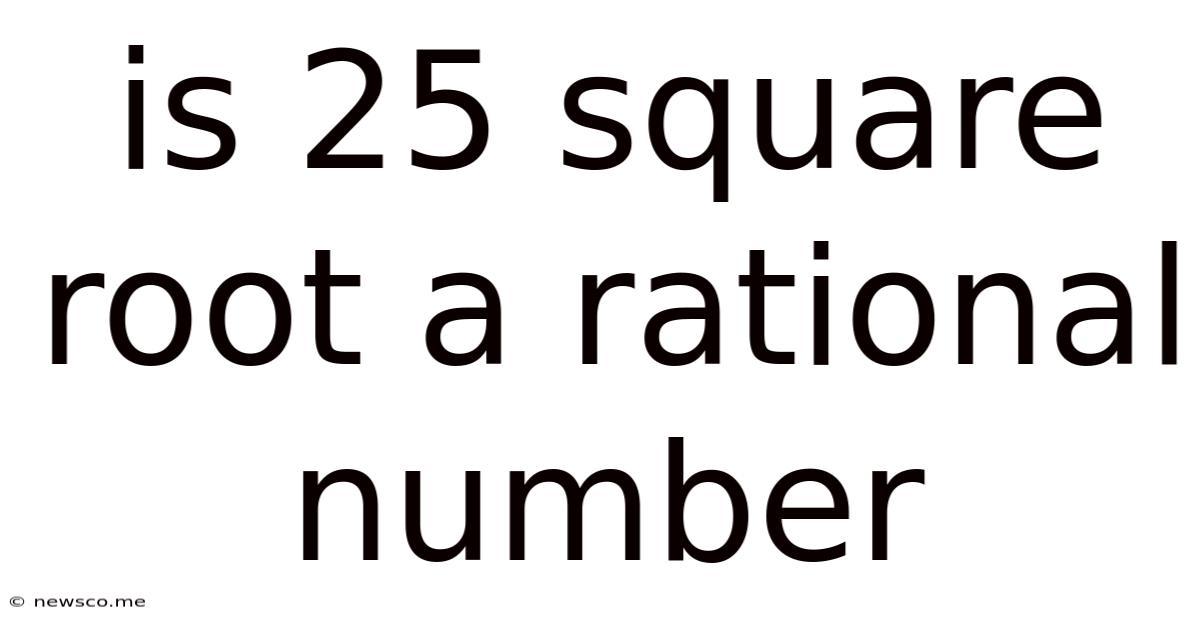
Table of Contents
- Is 25 Square Root A Rational Number
- Table of Contents
- Is the Square Root of 25 a Rational Number? A Deep Dive into Rational and Irrational Numbers
- Understanding Rational Numbers
- Understanding Irrational Numbers
- Square Roots and Rationality
- Perfect Squares and Rational Square Roots
- Non-Perfect Squares and Irrational Square Roots
- Answering the Question: Is √25 Rational?
- Further Exploration of Rational and Irrational Numbers
- Properties of Rational Numbers
- Properties of Irrational Numbers
- The Real Number System
- Identifying Rational and Irrational Numbers
- Practical Applications
- Conclusion: A Solid Understanding is Key
- Latest Posts
- Related Post
Is the Square Root of 25 a Rational Number? A Deep Dive into Rational and Irrational Numbers
The question, "Is the square root of 25 a rational number?" might seem simple at first glance. However, understanding the answer requires a deeper understanding of rational and irrational numbers, their properties, and how they relate to square roots. This comprehensive article will explore this question, providing a detailed explanation and examining related concepts.
Understanding Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p is the numerator and q is the non-zero denominator. In simpler terms, it's a number that can be written as a fraction. This includes:
- Integers: Whole numbers, both positive and negative (e.g., -3, 0, 5). These can be represented as fractions with a denominator of 1 (e.g., -3/1, 0/1, 5/1).
- Fractions: Numbers expressed as a ratio of two integers (e.g., 1/2, 3/4, -7/5).
- Terminating Decimals: Decimals that have a finite number of digits (e.g., 0.25, 0.75, 2.5). These can always be expressed as fractions.
- Repeating Decimals: Decimals with a pattern of digits that repeats infinitely (e.g., 0.333..., 0.142857142857...). These can also be expressed as fractions.
Examples of Rational Numbers:
- 1/2
- 3
- -4/7
- 0.75 (which is equivalent to 3/4)
- 0.333... (which is equivalent to 1/3)
Understanding Irrational Numbers
Irrational numbers are numbers that cannot be expressed as a fraction p/q of two integers. Their decimal representation is infinite and non-repeating. This means the digits go on forever without any discernible pattern.
Examples of Irrational Numbers:
- π (Pi): Approximately 3.14159..., but the digits continue infinitely without repeating.
- e (Euler's number): Approximately 2.71828..., also with infinitely non-repeating digits.
- √2 (Square root of 2): Approximately 1.41421..., an infinite non-repeating decimal.
Square Roots and Rationality
The square root of a number (x) is a value that, when multiplied by itself, equals x. For example, the square root of 9 is 3 because 3 * 3 = 9. Whether a square root is rational or irrational depends on the number being square-rooted.
Perfect Squares and Rational Square Roots
If the number under the square root symbol is a perfect square (the square of an integer), then its square root will be a rational number. A perfect square is a number that can be obtained by squaring an integer.
- Examples: 9 (33), 16 (44), 25 (55), 36 (66), etc.
The square root of each of these perfect squares is an integer, and integers are rational numbers.
Non-Perfect Squares and Irrational Square Roots
If the number under the square root symbol is not a perfect square, then its square root will be an irrational number.
- Examples: √2, √3, √5, √7, etc.
These square roots result in infinite, non-repeating decimal values.
Answering the Question: Is √25 Rational?
Now, let's return to our original question: Is the square root of 25 a rational number?
Since 25 is a perfect square (5 * 5 = 25), its square root is 5. The number 5 is an integer and can be expressed as the fraction 5/1. Therefore, the square root of 25 is a rational number.
Further Exploration of Rational and Irrational Numbers
Understanding the distinction between rational and irrational numbers is crucial in various mathematical fields. Here are some further points to consider:
Properties of Rational Numbers
- Closure under addition: The sum of two rational numbers is always a rational number.
- Closure under subtraction: The difference of two rational numbers is always a rational number.
- Closure under multiplication: The product of two rational numbers is always a rational number.
- Closure under division: The quotient of two rational numbers (excluding division by zero) is always a rational number.
These properties demonstrate the consistency and predictability of operations within the set of rational numbers.
Properties of Irrational Numbers
Irrational numbers, however, do not exhibit the same closure properties. For instance, the sum of a rational number and an irrational number is always irrational. Similarly, the product of a non-zero rational number and an irrational number is always irrational. The behavior of irrational numbers under arithmetic operations is more complex.
The Real Number System
Rational and irrational numbers together form the real number system. The real number system encompasses all numbers that can be plotted on a number line, including both rational and irrational numbers. It's a crucial foundation for many advanced mathematical concepts.
Identifying Rational and Irrational Numbers
When determining whether a number is rational or irrational, consider these points:
- Can it be expressed as a fraction of two integers? If yes, it's rational.
- Does its decimal representation terminate or repeat? If yes, it's rational.
- Does its decimal representation continue infinitely without repeating? If yes, it's irrational.
Practical Applications
The distinction between rational and irrational numbers extends beyond theoretical mathematics. It has practical applications in various fields, including:
- Engineering: Precision calculations often require understanding the limitations of representing irrational numbers with finite precision.
- Computer Science: Representing irrational numbers in computer systems involves approximations, which can introduce errors in calculations.
- Physics: Many physical constants, such as pi, are irrational numbers, requiring careful consideration in calculations.
Conclusion: A Solid Understanding is Key
The seemingly straightforward question about the rationality of √25 provides a valuable opportunity to explore the fundamental concepts of rational and irrational numbers. Understanding these concepts, their properties, and their applications is essential for anyone seeking a deeper understanding of mathematics and its relevance in the real world. The square root of 25, being a rational number, serves as a clear example of how a simple square root can be easily classified within the broader context of the real number system. Further study into these concepts will continue to reinforce this foundational knowledge and pave the way for more advanced mathematical explorations.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 25 Square Root A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.