Is 26 A Prime Or Composite Number
News Co
Apr 10, 2025 · 5 min read
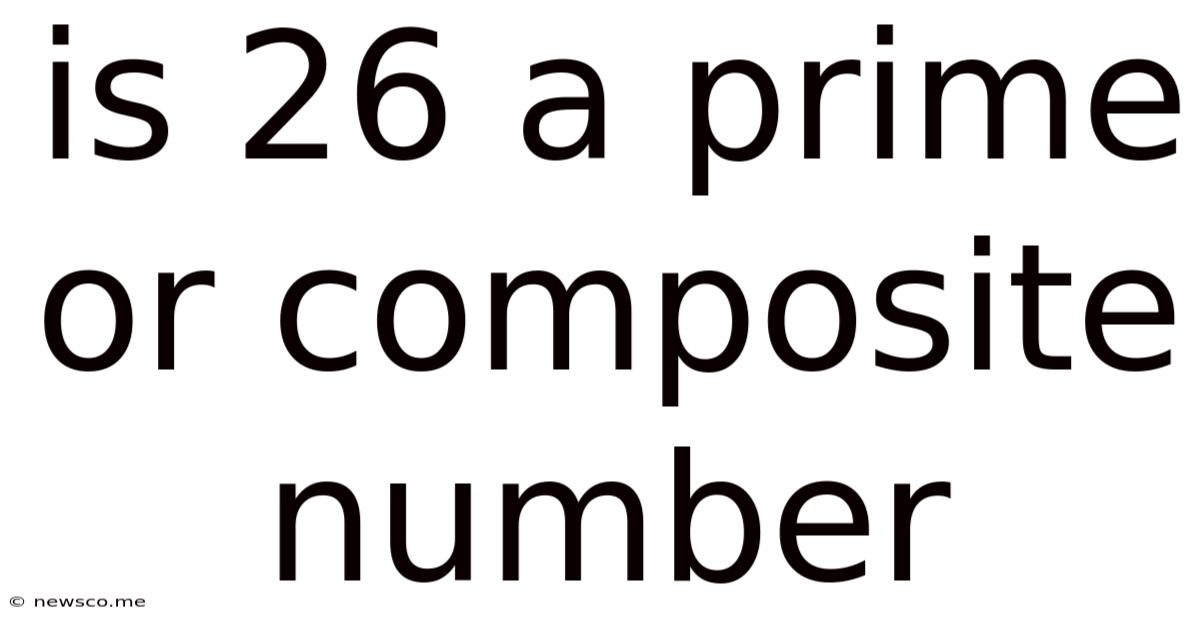
Table of Contents
Is 26 a Prime or Composite Number? A Deep Dive into Number Theory
Determining whether a number is prime or composite is a fundamental concept in number theory. While seemingly simple for smaller numbers, understanding the underlying principles allows us to tackle larger numbers and appreciate the elegance of mathematical classification. This article will explore whether 26 is prime or composite, delving into the definitions, properties, and methods used to identify such numbers. We'll also explore related concepts and applications of prime and composite numbers.
Understanding Prime and Composite Numbers
Before classifying 26, let's establish clear definitions:
-
Prime Number: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This means it's only divisible by 1 and itself without leaving a remainder. Examples include 2, 3, 5, 7, 11, and so on.
-
Composite Number: A composite number is a natural number greater than 1 that is not a prime number. In other words, it has at least one divisor other than 1 and itself. Examples include 4, 6, 8, 9, 10, and so on.
-
The Number 1: The number 1 is neither prime nor composite. It's a special case in number theory.
Determining if 26 is Prime or Composite
To determine whether 26 is prime or composite, we need to check if it has any divisors other than 1 and itself. Let's systematically investigate:
- Divisibility by 2: 26 is an even number, meaning it's divisible by 2. 26 ÷ 2 = 13.
Since 26 is divisible by 2 (and 13), it meets the definition of a composite number. It has divisors other than 1 and itself. Therefore, 26 is a composite number.
Methods for Identifying Prime and Composite Numbers
Several methods can be used to identify prime and composite numbers. These methods become particularly important when dealing with larger numbers where simple observation is insufficient.
1. Trial Division
This is the most straightforward method. We test for divisibility by all prime numbers up to the square root of the number in question. If no prime number divides the number without a remainder, the number is prime. Otherwise, it's composite. For 26, we only need to check divisibility by primes up to √26 ≈ 5.1. We find that 2 is a divisor, confirming that 26 is composite.
2. Sieve of Eratosthenes
This is an ancient algorithm for finding all prime numbers up to a specified integer. It works by iteratively marking as composite the multiples of each prime, starting with 2. The numbers remaining unmarked are prime. While effective for generating a list of primes, it's less efficient for individually testing a single number.
3. Primality Tests (for larger numbers)
For very large numbers, more sophisticated primality tests are necessary. These tests are probabilistic (meaning they provide a high probability of correctness, not absolute certainty) or deterministic (guaranteeing correctness). Examples include the Miller-Rabin test (probabilistic) and the AKS primality test (deterministic). These are beyond the scope of determining the primality of 26 but highlight the complexities involved with larger numbers.
The Importance of Prime and Composite Numbers
Prime and composite numbers aren't merely mathematical curiosities; they have far-reaching implications across various fields:
1. Cryptography
Prime numbers form the cornerstone of modern cryptography. Many encryption algorithms, such as RSA, rely on the difficulty of factoring large composite numbers into their prime factors. The security of online transactions and sensitive data hinges on the properties of prime numbers.
2. Number Theory and Abstract Algebra
Prime numbers are fundamental building blocks in number theory. They underpin concepts such as modular arithmetic, prime factorization, and the distribution of primes. Their properties are extensively studied in abstract algebra and related fields.
3. Computer Science
Prime numbers play a vital role in algorithm design and data structures. Hashing algorithms, for example, often utilize prime numbers to minimize collisions and improve efficiency.
4. Physics and Engineering
While less direct, prime numbers have found applications in areas like signal processing and the study of chaotic systems. The distribution of primes has connections to various physical phenomena.
Factors of 26 and Prime Factorization
The prime factorization of a number is its expression as a product of prime numbers. Since 26 is composite, we can find its prime factorization:
26 = 2 × 13
Both 2 and 13 are prime numbers. This prime factorization is unique for every composite number (Fundamental Theorem of Arithmetic).
Related Concepts
Several concepts are closely related to prime and composite numbers:
-
Divisibility Rules: These are shortcuts to determine divisibility by certain numbers without performing long division. For instance, a number is divisible by 2 if it's even, divisible by 3 if the sum of its digits is divisible by 3, and so on.
-
Greatest Common Divisor (GCD): The GCD of two or more numbers is the largest number that divides all of them without leaving a remainder. Algorithms like the Euclidean algorithm efficiently compute the GCD.
-
Least Common Multiple (LCM): The LCM of two or more numbers is the smallest number that is a multiple of all of them.
-
Perfect Numbers: A perfect number is a positive integer that is equal to the sum of its proper divisors (excluding itself). For example, 6 is a perfect number (1 + 2 + 3 = 6). The connection to prime numbers lies in the search for even perfect numbers, which are always of the form 2<sup>p-1</sup>(2<sup>p</sup> - 1), where 2<sup>p</sup> - 1 is a Mersenne prime.
-
Mersenne Primes: These are prime numbers of the form 2<sup>p</sup> - 1, where p is a prime number. Finding Mersenne primes is a significant challenge in number theory, and the Great Internet Mersenne Prime Search (GIMPS) project is dedicated to this pursuit.
Conclusion: 26 is definitively a composite number.
This comprehensive exploration of prime and composite numbers, focusing on the case of 26, reveals the fundamental nature of these concepts in mathematics and their far-reaching applications in various fields. Understanding the properties of prime and composite numbers is crucial for tackling more advanced mathematical concepts and solving problems in computer science, cryptography, and other disciplines. The seemingly simple question of whether 26 is prime or composite opens doors to a rich and fascinating world of number theory.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 26 A Prime Or Composite Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.