Is 29 Prime Or Composite Number
News Co
Mar 16, 2025 · 6 min read
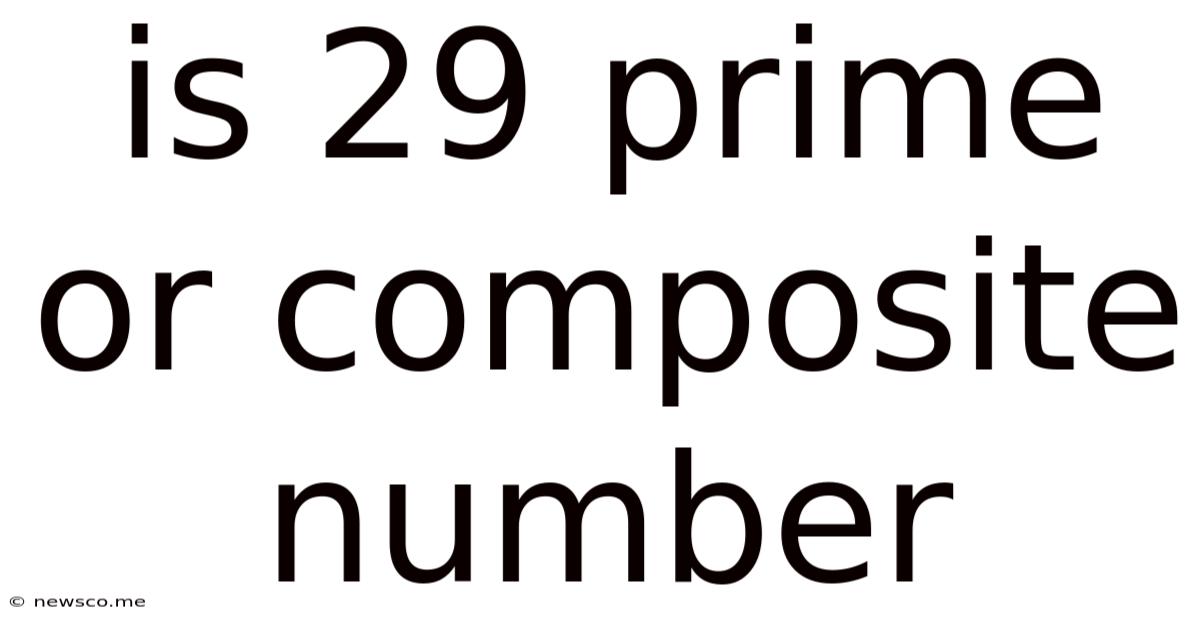
Table of Contents
Is 29 a Prime or Composite Number? A Deep Dive into Prime Numbers and Divisibility
Determining whether a number is prime or composite is a fundamental concept in number theory. This article will thoroughly explore the question: Is 29 a prime or composite number? We'll delve into the definitions, explore the methods for determining primality, and examine the significance of prime numbers in mathematics. By the end, you'll not only know the answer to the central question but also have a strong understanding of prime and composite numbers.
Understanding Prime and Composite Numbers
Before tackling the specific case of 29, let's establish a solid foundation by defining our key terms:
Prime Numbers: A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This means it's not divisible by any other whole number without leaving a remainder. Examples include 2, 3, 5, 7, 11, and so on. The number 1 is neither prime nor composite.
Composite Numbers: A composite number is a whole number greater than 1 that has more than two divisors. In other words, it can be divided evenly by at least one whole number other than 1 and itself. Examples include 4 (divisible by 1, 2, and 4), 6 (divisible by 1, 2, 3, and 6), 9 (divisible by 1, 3, and 9), and so on.
The Importance of Prime Numbers: Prime numbers are the building blocks of all other whole numbers. This fundamental property is enshrined in the Fundamental Theorem of Arithmetic, which states that every whole number greater than 1 can be uniquely expressed as a product of prime numbers. This theorem has profound implications in various areas of mathematics, including cryptography, coding theory, and algorithm design.
Determining if 29 is Prime or Composite
Now, let's focus on the number 29. To determine whether it's prime or composite, we need to check if it's divisible by any whole number other than 1 and itself.
We can start by checking the smallest prime numbers:
- Is 29 divisible by 2? No, because 29 is an odd number.
- Is 29 divisible by 3? No, because the sum of its digits (2 + 9 = 11) is not divisible by 3. This is a divisibility rule for 3.
- Is 29 divisible by 5? No, because it doesn't end in 0 or 5.
- Is 29 divisible by 7? No, 7 x 4 = 28, and 7 x 5 = 35. 29 lies between these multiples.
- Is 29 divisible by 11? No, 11 x 2 = 22, and 11 x 3 = 33. 29 lies between these multiples.
- Is 29 divisible by 13? No, 13 x 2 = 26, and 13 x 3 = 39. 29 lies between these multiples.
We can continue this process, but we only need to check prime numbers up to the square root of 29. The square root of 29 is approximately 5.38. Since we've already checked all primes up to 5 (2, 3, and 5), we can conclude that 29 is not divisible by any prime number less than its square root.
Therefore, 29 is a prime number. It only has two divisors: 1 and 29.
Methods for Determining Primality
There are several methods to determine whether a number is prime or composite:
1. Trial Division: This is the most basic method, as demonstrated above. We systematically test for divisibility by all prime numbers less than or equal to the square root of the number in question. While effective for smaller numbers, it becomes computationally expensive for very large numbers.
2. Sieve of Eratosthenes: This is a more efficient algorithm for finding all prime numbers up to a specified limit. It involves iteratively marking the multiples of each prime number, leaving only the primes unmarked.
3. Fermat Primality Test: This probabilistic test is based on Fermat's Little Theorem. It's faster than trial division for larger numbers but doesn't guarantee primality; it can sometimes produce false positives (composite numbers that pass the test).
4. Miller-Rabin Primality Test: This is another probabilistic test, but it's significantly more reliable than the Fermat test and less likely to produce false positives. It's widely used in cryptographic applications.
5. AKS Primality Test: This is a deterministic algorithm that provides a definite answer regarding the primality of a number. Unlike probabilistic tests, it doesn't rely on chance. However, it's computationally more expensive than probabilistic tests for very large numbers.
The Significance of Prime Numbers in Real-World Applications
The seemingly abstract nature of prime numbers belies their crucial role in various practical applications:
1. Cryptography: The security of many modern cryptographic systems relies heavily on the difficulty of factoring large numbers into their prime factors. Algorithms like RSA (Rivest–Shamir–Adleman) use the product of two very large prime numbers to generate encryption keys. The difficulty of factoring these large numbers makes it computationally infeasible to break the encryption.
2. Hashing Algorithms: Hash functions, used extensively in data security and integrity checks, often incorporate prime numbers to improve their distribution and collision resistance. A good hash function minimizes collisions (when different inputs produce the same output). The use of prime numbers contributes to this.
3. Random Number Generation: Prime numbers play a role in generating pseudo-random numbers, which are essential in simulations, statistical analysis, and various other applications. Algorithms used to generate these numbers often utilize prime numbers to ensure a more uniform distribution.
4. Coding Theory: Prime numbers are used in designing error-correcting codes, which are crucial for reliable data transmission and storage. These codes can detect and correct errors that may occur during transmission.
5. Digital Signal Processing: Prime numbers find applications in designing efficient digital filters and other signal processing algorithms. The use of prime numbers can improve the performance and reduce computational complexity.
Conclusion: 29 Remains Prime
We have definitively established that 29 is a prime number. This simple number, seemingly insignificant on its own, represents a fundamental building block within the vast landscape of mathematics. Its primality is not merely a theoretical curiosity; it reflects a deep mathematical truth that has far-reaching implications in various fields, impacting our daily lives in ways we may not even realize. Understanding prime numbers and their properties is crucial for appreciating the elegance and power of mathematics and its applications in the modern world. The exploration of primality continues to be a vibrant area of mathematical research, with ongoing efforts to develop more efficient algorithms and to uncover further properties of these fascinating numbers.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Is 29 Prime Or Composite Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.