Is 3 12 Equivalent To 1 4
News Co
Apr 23, 2025 · 5 min read
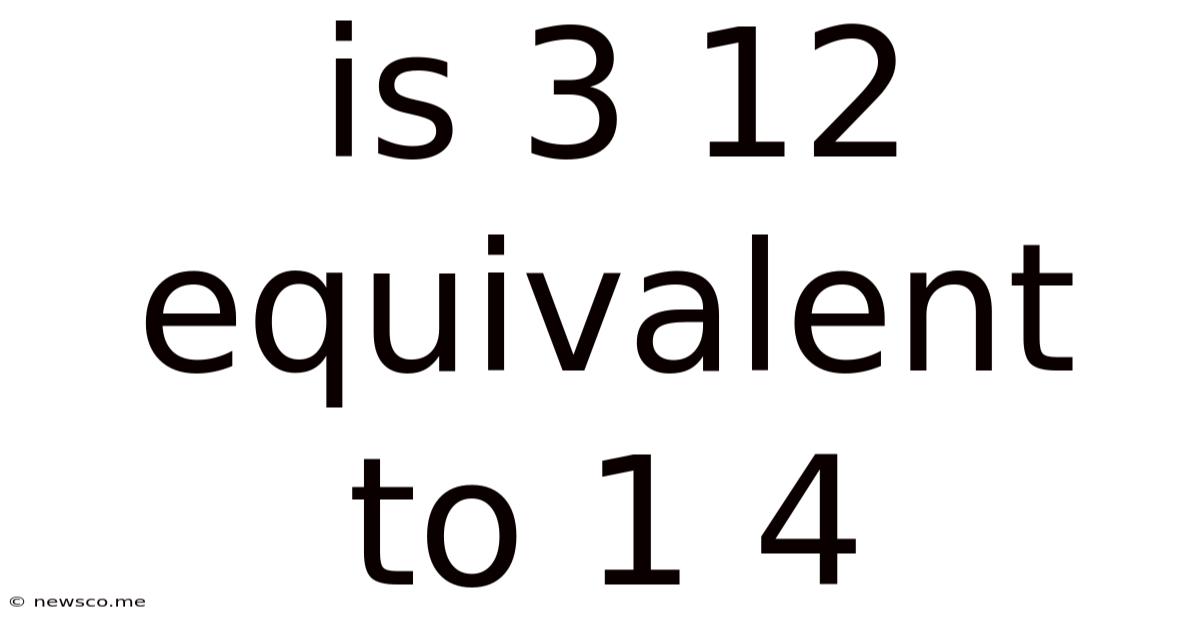
Table of Contents
Is 3/12 Equivalent to 1/4? A Deep Dive into Fraction Equivalence
The question, "Is 3/12 equivalent to 1/4?" might seem simple at first glance, especially for those comfortable with fractions. However, understanding the underlying concepts of fraction equivalence is crucial for a strong foundation in mathematics. This article will delve into this seemingly simple question, exploring the various methods to determine equivalence, the importance of simplification, and the broader implications within mathematics and real-world applications.
Understanding Fractions and Their Components
Before tackling the core question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/12, 3 is the numerator and 12 is the denominator. This means we have 3 parts out of a total of 12 equal parts.
Method 1: Simplification through Common Factors
The most straightforward way to determine if 3/12 is equivalent to 1/4 is by simplifying the fraction 3/12. Simplification involves dividing both the numerator and the denominator by their greatest common divisor (GCD).
The GCD of 3 and 12 is 3. Dividing both the numerator and the denominator by 3, we get:
3 ÷ 3 / 12 ÷ 3 = 1/4
Therefore, yes, 3/12 is equivalent to 1/4. Both fractions represent the same portion of a whole.
Method 2: Finding Equivalent Fractions through Multiplication
Another approach involves finding equivalent fractions by multiplying both the numerator and the denominator of a fraction by the same non-zero number.
Let's start with the fraction 1/4. If we multiply both the numerator and denominator by 3, we obtain:
1 x 3 / 4 x 3 = 3/12
This demonstrates that 1/4 and 3/12 are indeed equivalent fractions. Multiplying both parts of a fraction by the same number doesn't change its value; it simply represents the same proportion using different numbers.
Method 3: Visual Representation
Visual aids can be incredibly helpful in understanding fraction equivalence, particularly for those who benefit from a more concrete representation. Imagine a pizza cut into 12 slices. If you take 3 slices, you have 3/12 of the pizza.
Now, imagine the same pizza cut into only 4 slices. Taking one slice would represent 1/4 of the pizza. Visually comparing the two scenarios reveals that 3/12 and 1/4 represent the same amount of pizza.
The Importance of Simplifying Fractions
Simplifying fractions is essential for several reasons:
- Clarity: Simplified fractions are easier to understand and work with. 1/4 is clearly more concise and readily interpretable than 3/12.
- Efficiency: Simplified fractions make calculations simpler and faster. Imagine trying to add 3/12 and 5/12 versus adding 1/4 and 5/12. The simplified version is much more efficient.
- Standardization: In mathematics, it's customary to present fractions in their simplest form. This ensures consistency and avoids ambiguity.
Real-World Applications of Fraction Equivalence
The concept of fraction equivalence isn't confined to the realm of abstract mathematics. It has practical applications in numerous real-world scenarios:
- Cooking and Baking: Recipes often require precise measurements. Understanding fraction equivalence allows you to adjust ingredient amounts proportionally. If a recipe calls for 1/4 cup of sugar, you can substitute it with 3/12 cup.
- Construction and Engineering: Precise measurements are critical in construction and engineering. Fraction equivalence is crucial for accurate calculations and ensuring structural integrity.
- Finance: Understanding fractions and their equivalence is vital in financial calculations, particularly when dealing with percentages, interest rates, and proportions.
- Data Analysis: In data analysis, fractions are used extensively to represent proportions and percentages. Simplifying fractions allows for clearer interpretation and presentation of data.
Beyond the Basics: Exploring Further Concepts
The equivalence of 3/12 and 1/4 opens doors to exploring more advanced concepts within mathematics:
- Ratios and Proportions: Fractions are closely related to ratios and proportions. Understanding fraction equivalence is essential for solving problems involving ratios and proportions.
- Decimal Representation: Fractions can be converted to decimals, providing another way to represent the same value. Both 3/12 and 1/4 are equal to 0.25 in decimal form.
- Percentage Representation: Fractions can also be expressed as percentages. Both 3/12 and 1/4 represent 25%.
Common Mistakes and Misconceptions
While the equivalence of 3/12 and 1/4 is straightforward, some common misconceptions can arise:
- Incorrect Simplification: Students may incorrectly simplify fractions by dividing the numerator or denominator by a number that doesn't divide both evenly.
- Misunderstanding the Concept of Equivalence: Some students might struggle to grasp that equivalent fractions represent the same value despite having different numerators and denominators.
Conclusion: Mastering Fraction Equivalence
The seemingly simple question, "Is 3/12 equivalent to 1/4?" provides a gateway to understanding the fundamental concepts of fractions, simplification, and equivalence. Mastering these concepts is essential not only for academic success but also for navigating various aspects of daily life that involve proportions, ratios, and measurements. Through simplification, multiplication, and visual representation, we've demonstrated the clear equivalence of these two fractions. By understanding the underlying principles and avoiding common mistakes, you can confidently work with fractions in any context. The ability to recognize and manipulate equivalent fractions is a cornerstone of mathematical proficiency, paving the way for further exploration of more complex mathematical concepts. Remember to practice regularly to build a solid foundation and enhance your mathematical skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 3 12 Equivalent To 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.