Is 3 4 Equivalent To 6 8
News Co
May 02, 2025 · 5 min read
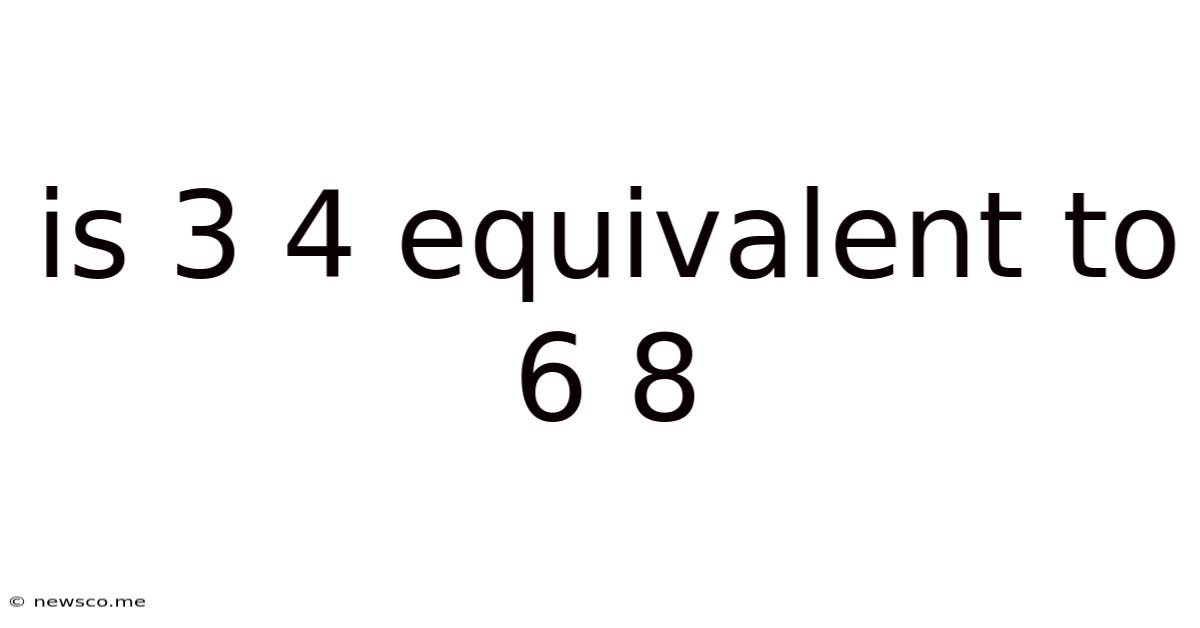
Table of Contents
Is 3/4 Equivalent to 6/8? A Deep Dive into Fraction Equivalence
The question, "Is 3/4 equivalent to 6/8?" might seem simple at first glance. For many, the answer is an immediate "yes." But understanding why this is true, and exploring the broader concepts of fraction equivalence, is crucial for a solid grasp of mathematical fundamentals. This article delves deep into this seemingly simple question, exploring the underlying principles and offering a comprehensive understanding of fraction equivalence, its applications, and its importance in various mathematical contexts.
Understanding Fractions: Parts of a Whole
Before diving into the equivalence of 3/4 and 6/8, let's establish a firm understanding of what fractions represent. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) represents three parts, and the denominator (4) signifies that the whole is divided into four equal parts. Therefore, 3/4 represents three out of four equal parts of a whole.
Exploring Fraction Equivalence: The Concept of Ratios
Two fractions are considered equivalent if they represent the same proportion or ratio. This means that even though the numerator and denominator might be different, the fractions represent the same value or portion of a whole. The key to understanding equivalence lies in the concept of simplifying fractions and the relationship between the numerator and denominator.
Simplifying Fractions: Finding the Simplest Form
Simplifying a fraction involves reducing it to its simplest form, where the numerator and denominator have no common factors other than 1. This is achieved by dividing both the numerator and the denominator by their greatest common divisor (GCD).
Let's take the fraction 6/8. The GCD of 6 and 8 is 2. Dividing both the numerator and denominator by 2 gives us:
6 ÷ 2 / 8 ÷ 2 = 3/4
This demonstrates that 6/8 is equivalent to 3/4 because both fractions represent the same proportion, even though they have different numerical values for the numerator and denominator. They both represent three out of four equal parts of a whole.
Visualizing Fraction Equivalence: The Power of Representation
Visual aids are incredibly helpful in understanding fraction equivalence. Imagine a pizza cut into four equal slices (representing the denominator of 3/4). If you take three of those slices, you have 3/4 of the pizza. Now imagine a similar pizza cut into eight equal slices (representing the denominator of 6/8). If you take six of these slices, you still have the same amount of pizza as before – three-quarters. This visual representation clearly demonstrates that 3/4 and 6/8 represent the same quantity.
Mathematical Proof of Equivalence: The Multiplicative Property
We can mathematically prove the equivalence of 3/4 and 6/8 using the multiplicative property of fractions. If we multiply both the numerator and denominator of a fraction by the same non-zero number, the value of the fraction remains unchanged.
Let's start with 3/4:
- Multiply the numerator and denominator by 2: (3 x 2) / (4 x 2) = 6/8
This clearly shows that multiplying 3/4 by 2/2 (which is equal to 1, thus not changing the value) results in 6/8. Conversely, if we divide the numerator and denominator of 6/8 by 2, we obtain 3/4.
Applications of Fraction Equivalence in Real-World Scenarios
Understanding fraction equivalence is not just an abstract mathematical concept; it has numerous real-world applications. Here are a few examples:
-
Cooking and Baking: Recipes often require adjustments based on the number of servings. If a recipe calls for 3/4 cup of flour, and you want to double the recipe, you'll need 6/8 cup of flour (equivalent to 1 1/2 cups).
-
Construction and Measurement: Construction workers frequently use fractions when measuring materials and distances. Knowing that 3/4 inch is equivalent to 6/8 inch ensures accurate measurements and prevents errors.
-
Data Analysis and Statistics: When working with proportions and percentages, understanding fraction equivalence is crucial for interpreting and comparing data correctly.
-
Finance and Budgeting: Fractions are often used to represent portions of a budget or financial statements. The ability to simplify and compare equivalent fractions aids in financial planning and decision-making.
Beyond 3/4 and 6/8: Exploring Other Equivalent Fractions
The principle of fraction equivalence extends far beyond the simple example of 3/4 and 6/8. Many other fractions can be shown to be equivalent using the same methods:
-
1/2 and 2/4 and 4/8: All these fractions represent one-half.
-
2/3 and 4/6 and 6/9: These fractions all represent two-thirds.
-
5/10 and 1/2: These fractions are equivalent, showing that simplifying fractions often reveals simpler representations of the same proportion.
Mastering Fraction Equivalence: Tips and Practice
Mastering fraction equivalence requires practice and a solid understanding of the underlying concepts. Here are some helpful tips:
-
Practice simplifying fractions: Regularly practice finding the GCD of the numerator and denominator and reducing fractions to their simplest form.
-
Use visual aids: Drawings, diagrams, and other visual representations can significantly enhance your understanding.
-
Solve practice problems: Work through various problems involving equivalent fractions to build your skills and confidence.
-
Understand the multiplicative property: Internalize the concept that multiplying or dividing both the numerator and denominator by the same non-zero number does not change the value of the fraction.
Conclusion: The Importance of Understanding Fraction Equivalence
The question "Is 3/4 equivalent to 6/8?" serves as a springboard for exploring the fundamental concepts of fraction equivalence. This article has demonstrated that they are indeed equivalent, using both visual representations and mathematical proofs. Understanding this concept is vital for a solid foundation in mathematics and has wide-ranging applications in various fields. By mastering fraction equivalence, you gain a valuable tool for solving problems, interpreting data, and navigating numerous real-world scenarios that involve proportions and ratios. Through consistent practice and the application of the principles discussed here, you can confidently tackle more complex fractional operations and further develop your mathematical skills. The seemingly simple question of fraction equivalence, therefore, unlocks a deeper understanding of fundamental mathematical principles with far-reaching practical applications.
Latest Posts
Latest Posts
-
Order Of Operations Worksheet Grade 6 Pdf
May 03, 2025
-
How Many Cc In A Cubic Meter
May 03, 2025
-
How To Write 75 On A Check
May 03, 2025
-
Find The Quotient H 6 H
May 03, 2025
-
Express The Interval Using Two Different Representations
May 03, 2025
Related Post
Thank you for visiting our website which covers about Is 3 4 Equivalent To 6 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.