Is 3/4 The Same As 2/3
News Co
Apr 26, 2025 · 5 min read
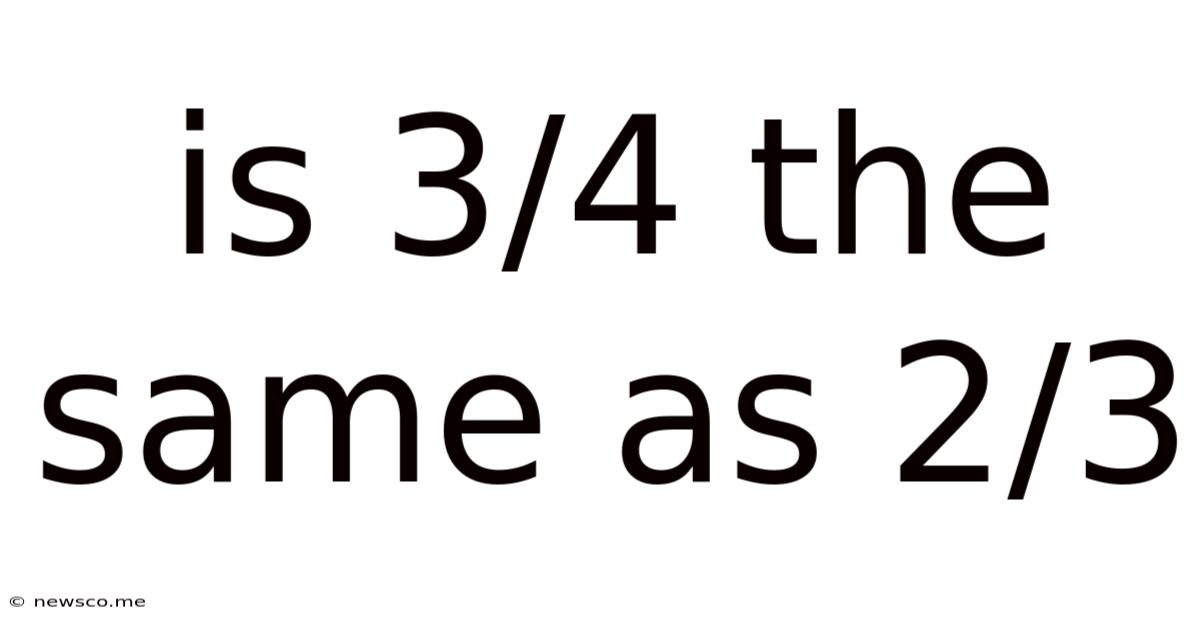
Table of Contents
Is 3/4 the Same as 2/3? A Deep Dive into Fraction Comparison
Are 3/4 and 2/3 the same? The short answer is no. While they might seem close, these fractions represent different portions of a whole. This article will delve deep into why they are different, exploring various methods to compare fractions and highlighting the crucial concepts of equivalent fractions, decimal representation, and visual representations to solidify your understanding. We'll also touch upon the practical applications of understanding fraction comparison.
Understanding Fractions: The Building Blocks
Before we directly compare 3/4 and 2/3, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) tells us we have three parts, and the denominator (4) tells us the whole is divided into four equal parts.
Comparing 3/4 and 2/3: The Methods
There are several ways to determine whether 3/4 is equal to 2/3:
1. Finding a Common Denominator
This is arguably the most common and straightforward method. To compare fractions, we need to express them with the same denominator. We find the least common multiple (LCM) of the denominators 4 and 3. The LCM of 4 and 3 is 12.
- Converting 3/4: To get a denominator of 12, we multiply both the numerator and the denominator by 3: (3 x 3) / (4 x 3) = 9/12.
- Converting 2/3: To get a denominator of 12, we multiply both the numerator and the denominator by 4: (2 x 4) / (3 x 4) = 8/12.
Now that we have the fractions with a common denominator, we can clearly see that 9/12 is greater than 8/12. Therefore, 3/4 is not the same as 2/3.
2. Converting to Decimals
Another effective way to compare fractions is by converting them to decimals. We simply divide the numerator by the denominator:
- 3/4: 3 ÷ 4 = 0.75
- 2/3: 2 ÷ 3 = 0.666... (a repeating decimal)
Comparing the decimal values, 0.75 is clearly greater than 0.666..., again demonstrating that 3/4 is larger than 2/3.
3. Visual Representation
Visualizing fractions can be incredibly helpful, especially for grasping the concept intuitively. Imagine a pizza cut into four equal slices (representing the denominator of 3/4). 3/4 represents having three of those four slices.
Now imagine a different pizza cut into three equal slices (representing the denominator of 2/3). 2/3 represents having two of those three slices. Even visually, it's apparent that three-quarters of a pizza is more than two-thirds of a pizza. This visual method reinforces the fact that 3/4 and 2/3 are not equivalent.
Why Understanding Fraction Comparison is Crucial
The ability to accurately compare fractions is fundamental to various mathematical concepts and real-world applications. It's essential for:
- Solving mathematical problems: Many mathematical problems, particularly in algebra and calculus, require comparing and manipulating fractions.
- Baking and Cooking: Recipes often involve fractional measurements. Understanding fraction comparison ensures accurate ingredient proportions.
- Construction and Engineering: Precision is paramount in these fields. Comparing fractions helps in accurate measurements and calculations.
- Data Analysis: Understanding fractions is critical for interpreting data represented as fractions or percentages.
- Financial Calculations: Fractions are frequently used in financial calculations involving interest rates, shares, and other financial instruments.
Beyond the Basics: Equivalent Fractions and Simplification
It's important to understand the concept of equivalent fractions. Equivalent fractions represent the same portion of a whole, even though they have different numerators and denominators. For instance, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions. They all represent one-half.
Simplifying fractions, or reducing them to their lowest terms, is another essential skill. This involves dividing both the numerator and the denominator by their greatest common divisor (GCD). For example, 6/9 can be simplified to 2/3 by dividing both the numerator and denominator by 3 (their GCD). Simplifying fractions makes them easier to compare and work with.
Common Mistakes to Avoid When Comparing Fractions
Several common pitfalls can lead to incorrect fraction comparisons:
- Focusing solely on numerators or denominators: Comparing only the numerators or denominators without considering both is a common mistake. Remember, both components are crucial in determining the value of a fraction.
- Incorrectly finding common denominators: Mistakes in finding the least common multiple (LCM) can lead to inaccurate comparisons.
- Ignoring the concept of equivalent fractions: Failing to recognize equivalent fractions can lead to misinterpretations and errors in comparisons.
- Rounding errors in decimal conversions: When converting to decimals, be mindful of repeating decimals and avoid premature rounding, which can lead to inaccuracies in comparison.
Practical Applications: Real-World Examples
Let's explore a couple of real-world scenarios where understanding fraction comparison is vital:
Scenario 1: Sharing a Pizza
Imagine you and two friends order a pizza. One friend wants 3/4 of the pizza, while you and the other friend want to split the remaining portion equally. To determine if you can divide the remainder equally, you need to compare the fractions. Since 3/4 leaves 1/4 remaining, and 1/4 can be divided by two, this is possible.
Scenario 2: Building a Shelf
You're building a shelf, and the instructions call for a board that's 2/3 of a meter long. You have a board that's 3/4 of a meter long. Comparing these fractions reveals that the 3/4 meter board is longer than required; the difference is 1/12 of a meter.
Conclusion: Mastering Fraction Comparison
Comparing fractions, while seemingly simple, is a fundamental skill with far-reaching applications. By understanding the different methods – finding common denominators, converting to decimals, and using visual representations – you can confidently and accurately compare any two fractions. Remember to avoid common pitfalls, practice regularly, and apply your knowledge to real-world problems to truly master this essential mathematical concept. The ability to compare fractions with accuracy is a testament to a strong mathematical foundation and empowers you to tackle more complex mathematical challenges with confidence.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 3/4 The Same As 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.