Is 4 10 Equivalent To 2 5
News Co
Mar 18, 2025 · 5 min read
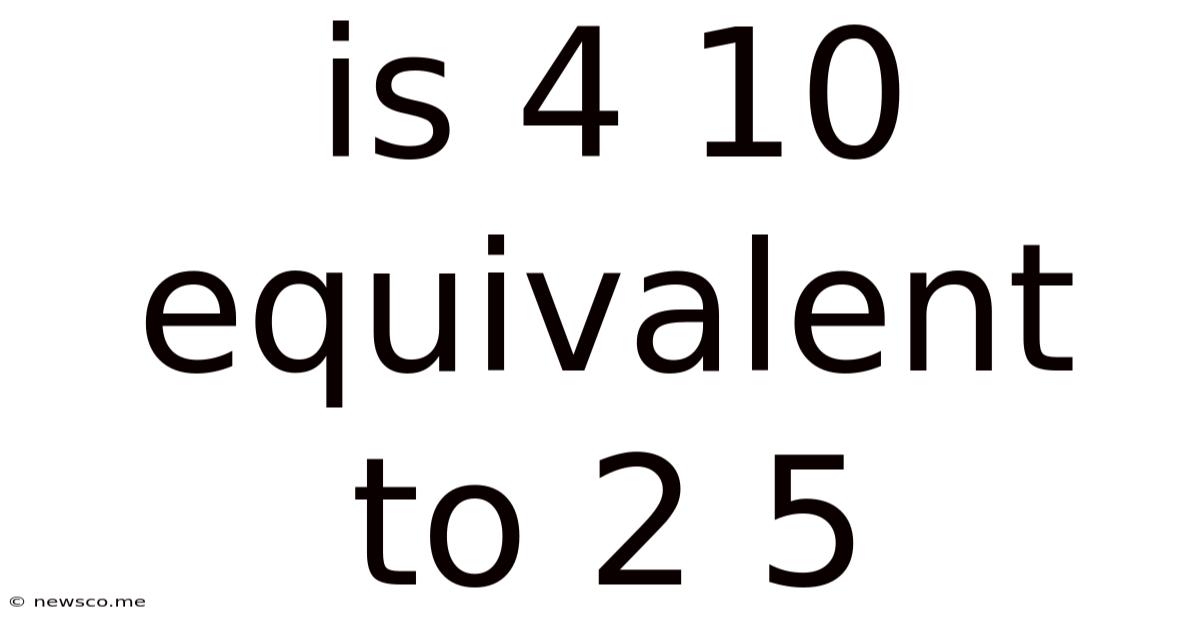
Table of Contents
Is 4:10 Equivalent to 2:5? A Deep Dive into Ratio and Proportion
The question, "Is 4:10 equivalent to 2:5?" might seem simple at first glance. It touches upon fundamental mathematical concepts of ratio and proportion, concepts crucial for numerous applications in various fields, from cooking and construction to advanced scientific research. This article will not only answer this specific question but also explore the broader implications of understanding ratios and proportions. We will delve into different methods for determining equivalence, explore common mistakes, and provide real-world examples to solidify your understanding.
Understanding Ratios
A ratio is a comparison of two or more quantities. It shows the relative size of one quantity compared to another. Ratios are often expressed in several ways:
- Using a colon: 4:10 (read as "4 to 10")
- As a fraction: 4/10
- Using the word "to": 4 to 10
In our example, 4:10 represents the ratio of 4 units of something to 10 units of something else. The key is the relative relationship, not the absolute values.
Understanding Proportions
A proportion states that two ratios are equal. It expresses the equality between two ratios. For example, if we have two ratios, a:b and c:d, then a proportion would be written as:
a:b = c:d or a/b = c/d
This means that the relationship between 'a' and 'b' is the same as the relationship between 'c' and 'd'.
Determining Equivalence: Methods and Techniques
Several methods can be used to determine if two ratios are equivalent, thereby forming a proportion. Let's explore the most common ones:
1. Simplification to Lowest Terms
This is arguably the most straightforward approach. We simplify each ratio by dividing both parts by their greatest common divisor (GCD).
Let's analyze 4:10 and 2:5:
- Ratio 1 (4:10): The GCD of 4 and 10 is 2. Dividing both by 2 gives us 2:5.
- Ratio 2 (2:5): This ratio is already in its simplest form.
Since simplifying 4:10 results in 2:5, the two ratios are equivalent.
2. Cross-Multiplication
Cross-multiplication is a powerful technique for verifying the equality of two ratios. If we have a:b = c:d, then cross-multiplying gives us:
a * d = b * c
Let's apply this to our example:
4:10 = 2:5
Cross-multiplying:
4 * 5 = 10 * 2
20 = 20
Since the equation holds true, the ratios 4:10 and 2:5 are indeed equivalent.
3. Decimal Conversion
We can convert each ratio to its decimal equivalent. If the decimal values are the same, the ratios are equivalent.
- Ratio 1 (4:10): 4/10 = 0.4
- Ratio 2 (2:5): 2/5 = 0.4
Both ratios have a decimal value of 0.4, confirming their equivalence.
Common Mistakes to Avoid
While the concept of ratios and proportions is relatively simple, some common pitfalls can lead to errors:
- Ignoring units: Always consider the units involved. A ratio of 4 apples to 10 oranges is different from a ratio of 4 apples to 10 apples. Inconsistent units invalidate comparisons.
- Incorrect simplification: Ensure you're dividing by the greatest common divisor. Failing to do so may lead to incorrect conclusions.
- Confusing ratios with fractions: While ratios can be expressed as fractions, they represent a comparison of quantities, while fractions represent parts of a whole. The context is crucial.
- Misunderstanding cross-multiplication: Cross-multiplication only works for testing the equivalence of two ratios. It's not a method for solving a proportion involving an unknown variable.
Real-World Applications of Ratios and Proportions
The principles of ratio and proportion find widespread use across numerous fields:
1. Cooking and Baking: Recipes frequently use ratios. If a recipe calls for a 2:1 ratio of flour to sugar, and you want to double the recipe, you must maintain that ratio.
2. Construction and Engineering: Blueprints and scale models rely heavily on ratios and proportions to accurately represent larger structures.
3. Mapmaking: Maps use a scale (e.g., 1:100,000) to represent distances proportionally. This ratio ensures accurate representation of geographical features.
4. Finance: Interest rates, currency exchange rates, and stock market ratios all utilize ratio and proportion calculations.
5. Science: In many scientific experiments, maintaining precise ratios of reactants or calculating concentrations relies heavily on this concept.
6. Photography: The aperture setting on a camera, expressed as f-stops (e.g., f/2.8, f/4), represents ratios that control the amount of light reaching the sensor.
7. Medicine: Dosage calculations in medicine often involve the precise use of ratios and proportions to ensure patient safety.
Expanding on the Concept: Proportional Reasoning
Understanding ratios and proportions forms the basis of proportional reasoning, a vital cognitive skill. It involves the ability to:
- Identify proportional relationships: recognizing situations where quantities change in a consistent ratio.
- Solve proportions: Finding missing values in a proportional relationship.
- Apply proportional reasoning: using proportional relationships to solve real-world problems.
Conclusion: More Than Just Numbers
The question of whether 4:10 is equivalent to 2:5 is a gateway to understanding the powerful concepts of ratio and proportion. These concepts aren't merely abstract mathematical ideas; they are practical tools used daily in countless ways. By mastering these concepts, you equip yourself with a crucial skillset applicable across various disciplines and everyday scenarios. The ability to identify, manipulate, and apply ratios and proportions is a cornerstone of mathematical literacy and problem-solving prowess. So, yes, 4:10 is indeed equivalent to 2:5 – a simple truth with far-reaching implications.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 4 10 Equivalent To 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.