Is 4 5 Equal To 8 10
News Co
Apr 21, 2025 · 6 min read
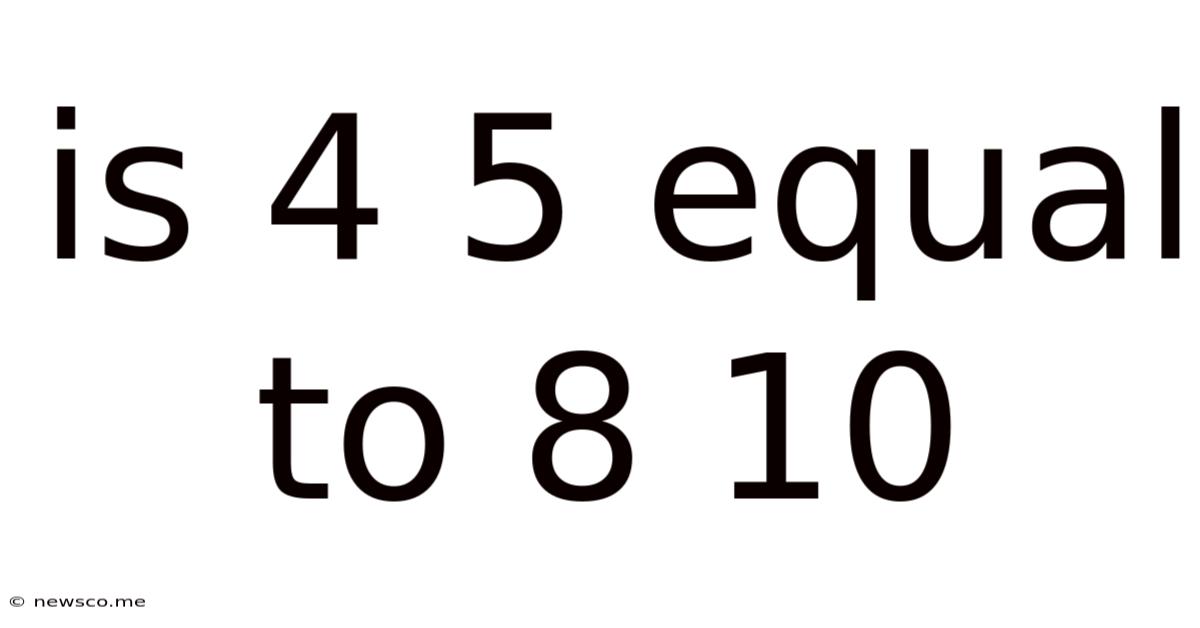
Table of Contents
Is 4/5 Equal to 8/10? A Deep Dive into Equivalent Fractions
The question, "Is 4/5 equal to 8/10?" might seem simple at first glance, particularly for those well-versed in mathematics. However, understanding the underlying principles behind this equivalence is crucial for grasping fundamental concepts in fractions, ratios, and proportional reasoning. This article will not only answer the question definitively but also explore the broader implications of equivalent fractions, their applications, and how to identify them.
Understanding Fractions: A Quick Recap
Before diving into the specifics of 4/5 and 8/10, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 3/4, the numerator (3) represents three parts, and the denominator (4) signifies that the whole is divided into four equal parts.
Equivalent Fractions: The Concept of Equality
Equivalent fractions represent the same proportion or value, even though they look different. They are essentially different ways of expressing the same part of a whole. The key to understanding equivalent fractions is recognizing that multiplying or dividing both the numerator and the denominator by the same non-zero number does not change the value of the fraction.
This principle is fundamental to simplifying fractions (reducing them to their lowest terms) and finding common denominators when adding or subtracting fractions.
Is 4/5 Equal to 8/10? The Proof
Let's now address the central question: Is 4/5 equal to 8/10? The answer is a resounding yes. Here's why:
If we multiply both the numerator and the denominator of 4/5 by 2, we get:
(4 x 2) / (5 x 2) = 8/10
Since we performed the same operation (multiplication by 2) on both parts of the fraction, the value remains unchanged. Therefore, 4/5 and 8/10 are equivalent fractions, representing the same proportion or quantity.
Conversely, we can also simplify 8/10 by dividing both the numerator and the denominator by their greatest common divisor, which is 2:
(8 ÷ 2) / (10 ÷ 2) = 4/5
This demonstrates that simplifying 8/10 leads us back to 4/5, further confirming their equivalence.
Visual Representation: Understanding Through Images
Visual aids can significantly enhance comprehension. Imagine a pizza cut into 5 equal slices. If you eat 4 slices, you've consumed 4/5 of the pizza.
Now, imagine the same pizza cut into 10 equal slices. If you eat 8 slices, you've still consumed the same amount – 8/10 or 4/5 of the pizza. Both fractions represent the same portion of the whole.
This visual representation makes the equivalence more intuitive and easier to grasp, particularly for those who find abstract mathematical concepts challenging.
Applications of Equivalent Fractions in Real-World Scenarios
Understanding equivalent fractions is not merely an academic exercise; it has numerous practical applications in various real-world scenarios:
-
Cooking and Baking: Recipes often require adjusting ingredient quantities. Knowing how to work with equivalent fractions allows you to easily scale recipes up or down while maintaining the correct proportions. For instance, if a recipe calls for 1/2 cup of sugar and you want to double the recipe, you'll need 1/2 + 1/2 = 1 cup, or using equivalent fractions, you can easily convert this to 2/4, 3/6, 4/8 and so on. This makes adjusting ingredient amounts intuitive.
-
Construction and Engineering: Accurate measurements are crucial in construction and engineering. Equivalent fractions help in converting measurements between different units and ensuring precision in calculations. This is particularly important when working with blueprints and scaling drawings.
-
Finance and Budgeting: Working with percentages, which are essentially fractions (e.g., 50% = 50/100 = 1/2), relies heavily on understanding equivalent fractions. Calculating discounts, interest rates, and other financial aspects involves manipulating and comparing fractions.
-
Data Analysis and Statistics: In data analysis and statistics, equivalent fractions are instrumental in simplifying and interpreting data. They allow for consistent comparisons and facilitate the understanding of proportions and ratios within datasets.
-
Everyday Life: From dividing a cake among friends to sharing resources equitably, the concept of equivalent fractions implicitly underpins many of our daily activities. Understanding them allows for fairer and more accurate distributions.
Beyond the Basics: Exploring More Complex Equivalent Fractions
While the example of 4/5 and 8/10 is relatively straightforward, the concept extends to more complex fractions. Finding equivalent fractions often involves simplifying complex fractions, finding a common denominator for addition and subtraction, and making comparisons between ratios.
For example, consider the fractions 12/18 and 2/3. Are they equivalent? Let's find out:
Simplifying 12/18 by dividing both the numerator and denominator by their greatest common divisor (6), we get:
(12 ÷ 6) / (18 ÷ 6) = 2/3
This confirms that 12/18 and 2/3 are equivalent fractions.
Identifying Equivalent Fractions: Methods and Techniques
Several methods exist for determining if two fractions are equivalent:
-
Cross-Multiplication: This is a quick method to verify equivalence. Cross-multiply the numerator of one fraction with the denominator of the other, and vice-versa. If the products are equal, the fractions are equivalent. For instance, for 4/5 and 8/10:
4 x 10 = 40 5 x 8 = 40
Since the products are equal, the fractions are equivalent.
-
Simplifying Fractions: Reduce both fractions to their simplest forms (lowest terms) by dividing both the numerator and denominator by their greatest common divisor. If both simplified fractions are identical, they are equivalent.
-
Finding a Common Denominator: Convert both fractions to equivalent fractions with the same denominator. If the numerators are also equal, the original fractions are equivalent.
Conclusion: Mastering Equivalent Fractions for Mathematical Proficiency
Understanding equivalent fractions is a cornerstone of mathematical proficiency. It's not just about knowing that 4/5 is equal to 8/10; it's about grasping the underlying principle of maintaining proportionality despite changes in representation. This fundamental concept permeates various aspects of mathematics and extends into numerous real-world applications. By mastering equivalent fractions, you equip yourself with a powerful tool for problem-solving and critical thinking, enhancing your understanding of ratios, proportions, and numerical relationships. The ability to recognize and manipulate equivalent fractions is essential for success in various fields, from cooking and baking to engineering and finance, highlighting its practical significance in everyday life. So, the next time you encounter a fraction, remember the importance of recognizing and working with its equivalent forms – it's a skill that will serve you well in many facets of your life.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 4 5 Equal To 8 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.