Is 4 6 Equal To 2 3
News Co
Apr 06, 2025 · 5 min read
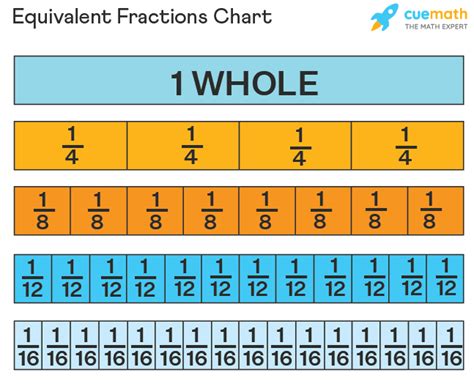
Table of Contents
Is 4/6 Equal to 2/3? A Deep Dive into Fraction Simplification
The question, "Is 4/6 equal to 2/3?" might seem simple at first glance. For many, the answer is an immediate yes. However, understanding why this is true, and the broader implications of fraction simplification, is crucial for a solid grasp of mathematical concepts. This article will delve into this seemingly simple equation, exploring the underlying principles of equivalent fractions, simplifying fractions, and the importance of understanding these concepts in various mathematical contexts.
Understanding Fractions: Numerator and Denominator
Before diving into the equivalence of 4/6 and 2/3, let's establish a strong foundation. A fraction represents a part of a whole. It consists of two key components:
- Numerator: The top number indicates the number of parts we have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
For instance, in the fraction 4/6, the numerator (4) signifies that we possess four parts, while the denominator (6) means the whole is divided into six equal parts. Similarly, in 2/3, we have two parts out of a total of three equal parts.
Equivalent Fractions: The Concept of Equality
Equivalent fractions represent the same proportion or value, even though they look different. They represent the same point on the number line. Think of cutting a pizza: If you cut it into six slices and take four, it's the same amount as cutting it into three slices and taking two. This illustrates the core concept of equivalent fractions. We can obtain equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number.
This is the fundamental principle at play when we say 4/6 is equal to 2/3. We're not changing the value of the fraction; we're simply expressing it in a simpler form.
Simplifying Fractions: Finding the Lowest Terms
Simplifying a fraction, also known as reducing a fraction to its lowest terms, means expressing the fraction using the smallest possible whole numbers in the numerator and denominator. This process doesn't alter the value of the fraction; it merely presents it in a more concise and manageable form.
To simplify a fraction, we find the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. We then divide both the numerator and denominator by the GCD.
Let's apply this to 4/6:
-
Find the GCD of 4 and 6: The factors of 4 are 1, 2, and 4. The factors of 6 are 1, 2, 3, and 6. The greatest common factor is 2.
-
Divide both the numerator and denominator by the GCD: 4 ÷ 2 = 2 and 6 ÷ 2 = 3.
Therefore, the simplified form of 4/6 is 2/3. This confirms that 4/6 and 2/3 are indeed equivalent fractions.
Visualizing Equivalent Fractions
Visual representations can significantly enhance understanding. Imagine a rectangle divided into six equal parts. If you shade four of these parts, you visually represent 4/6. Now, imagine grouping these six parts into pairs. You'll have three groups, with two shaded groups out of three total groups. This visually demonstrates that 4/6 is equivalent to 2/3. This visual approach helps solidify the concept beyond abstract mathematical operations.
The Importance of Simplifying Fractions
Simplifying fractions is not merely an exercise in tidiness; it offers several crucial benefits:
-
Easier Calculations: Simplified fractions make calculations significantly easier, particularly when adding, subtracting, multiplying, or dividing fractions. Working with smaller numbers reduces the risk of errors and simplifies the computation process.
-
Better Understanding: Simplified fractions provide a clearer understanding of the proportion represented. The simplified form gives a more intuitive grasp of the magnitude of the fraction.
-
Standardized Form: Presenting fractions in their simplest form ensures consistency and facilitates easy comparison between different fractions. This is particularly important in various fields like engineering, physics, and finance where accuracy and clarity are paramount.
Beyond 4/6 and 2/3: Applying the Principles
The principles discussed extend far beyond the simple example of 4/6 and 2/3. Consider these examples:
-
12/18: The GCD of 12 and 18 is 6. Dividing both by 6 simplifies the fraction to 2/3.
-
15/25: The GCD of 15 and 25 is 5. Dividing both by 5 simplifies the fraction to 3/5.
-
24/36: The GCD of 24 and 36 is 12. Dividing both by 12 simplifies the fraction to 2/3.
Notice that several fractions, when simplified, reduce to the same equivalent fraction. This highlights the interconnectedness of fractions and the importance of understanding simplification for effective mathematical manipulation.
Real-world Applications
The concept of equivalent fractions and simplification isn't confined to the classroom; it has numerous practical applications in various aspects of daily life:
-
Cooking and Baking: Recipes often involve fractions. Simplifying fractions helps in adjusting ingredient quantities accurately. If a recipe calls for 4/6 cup of sugar, simplifying it to 2/3 cup makes measuring easier.
-
Construction and Engineering: Precise measurements are essential in construction and engineering. Fractions play a significant role, and their simplification ensures accurate calculations and prevents errors that could have significant consequences.
-
Finance and Economics: Financial calculations frequently involve fractions, whether dealing with percentages, interest rates, or ratios. Simplifying fractions enhances clarity and reduces the possibility of mistakes in complex financial analyses.
Conclusion: The Significance of Understanding Fraction Equivalence
The seemingly simple question, "Is 4/6 equal to 2/3?", opens the door to a deeper understanding of fundamental mathematical concepts. This article has explored the principles of equivalent fractions, the process of simplification, and its real-world relevance. Mastering these concepts is not just about solving mathematical problems; it's about developing a robust foundation in mathematical reasoning, crucial for success in various academic and professional pursuits. Remember, understanding the "why" behind mathematical operations is just as vital as knowing the "how." This deeper understanding enhances problem-solving skills and cultivates a more profound appreciation for the elegance and power of mathematics. The equivalence of 4/6 and 2/3, therefore, serves as a gateway to a broader understanding of the world of fractions and their applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 4 6 Equal To 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.