Is 6 8 Equal To 3 4
News Co
May 08, 2025 · 5 min read
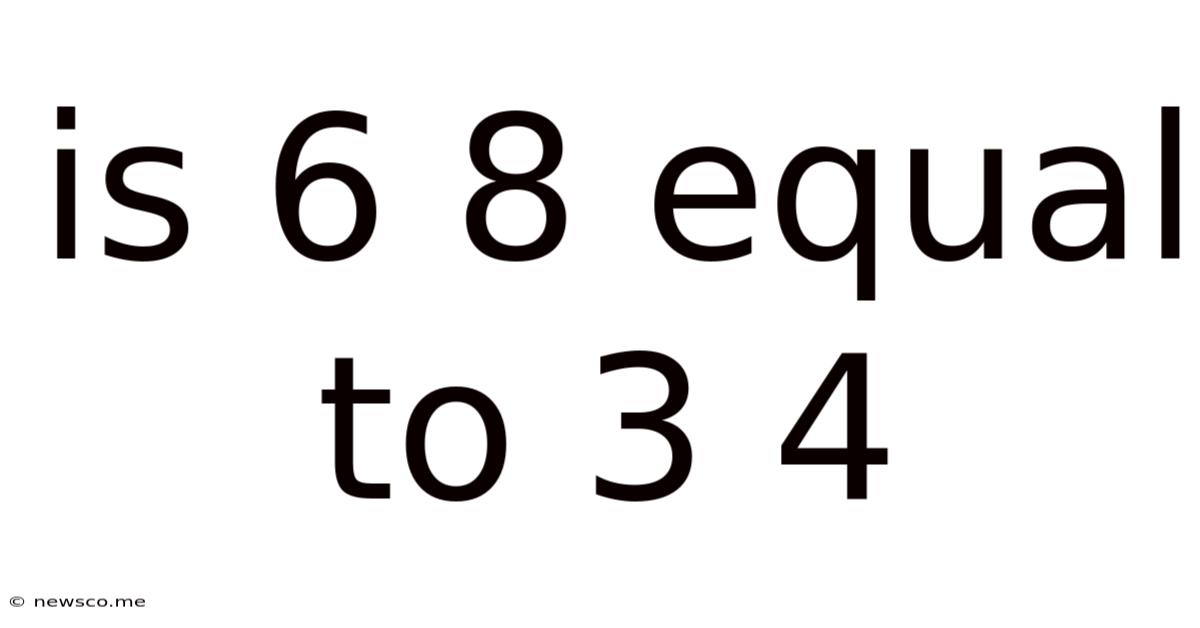
Table of Contents
Is 6/8 Equal to 3/4? A Deep Dive into Fraction Simplification
The question, "Is 6/8 equal to 3/4?" is a fundamental concept in mathematics, specifically in the realm of fractions. While the answer might seem obvious to some, understanding the underlying principles behind fraction simplification is crucial for grasping more advanced mathematical concepts. This article will delve into the intricacies of this seemingly simple question, exploring equivalent fractions, the greatest common divisor (GCD), and the significance of simplifying fractions in various mathematical applications.
Understanding Fractions: A Quick Recap
Before we tackle the core question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 parts out of a total of 4 equal parts.
Equivalent Fractions: The Foundation of Simplification
Equivalent fractions are fractions that represent the same value, even though they look different. They are created by multiplying or dividing both the numerator and the denominator by the same non-zero number. For example, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions because they all represent one-half. This principle is essential for simplifying fractions and comparing their values.
Simplifying Fractions: Finding the Simplest Form
Simplifying a fraction means reducing it to its simplest form, where the numerator and denominator have no common factors other than 1. This process ensures that the fraction is expressed in the most concise and efficient manner. Simplifying fractions makes calculations easier and improves understanding.
The Role of the Greatest Common Divisor (GCD)
The key to simplifying fractions lies in finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Once the GCD is found, both the numerator and the denominator are divided by the GCD to obtain the simplified fraction.
Example: Let's consider the fraction 6/8.
- Find the factors of 6: 1, 2, 3, 6
- Find the factors of 8: 1, 2, 4, 8
- Identify the common factors: 1 and 2
- Determine the greatest common factor (GCF): 2 is the GCD of 6 and 8.
- Simplify the fraction: Divide both the numerator and the denominator by the GCD (2): 6 ÷ 2 = 3 and 8 ÷ 2 = 4.
Therefore, the simplified fraction is 3/4.
Is 6/8 Equal to 3/4? The Definitive Answer
Yes, 6/8 is equal to 3/4. As demonstrated above, simplifying the fraction 6/8 by dividing both the numerator and denominator by their GCD (2) results in the equivalent fraction 3/4. This confirms that both fractions represent the same proportion or value.
The Importance of Simplifying Fractions
Simplifying fractions is not merely a mathematical exercise; it has significant implications in various fields:
-
Improved Clarity and Understanding: Simplified fractions are easier to interpret and understand. For example, 3/4 is clearly more intuitive than 6/8, especially when comparing fractions or performing calculations.
-
Easier Calculations: Working with simplified fractions makes arithmetic operations like addition, subtraction, multiplication, and division significantly easier and less prone to errors.
-
Real-world Applications: Simplifying fractions is essential in various real-world scenarios, such as measuring ingredients in cooking, calculating proportions in construction, or understanding data in statistics.
-
Foundation for Advanced Mathematics: A solid understanding of fraction simplification is crucial for mastering more advanced mathematical concepts, including algebra, calculus, and geometry. It forms the basis for working with ratios, proportions, and percentages.
Beyond Simplification: Visualizing Fractions
Visual aids can help solidify the understanding of equivalent fractions. Imagine a pizza cut into 8 slices. If you take 6 slices, you have 6/8 of the pizza. Now imagine the same pizza cut into 4 slices. If you take 3 slices, you still have the same amount of pizza – 3/4. This visual representation clearly demonstrates the equivalence of 6/8 and 3/4.
Common Mistakes to Avoid
-
Incorrectly identifying the GCD: Failing to find the greatest common divisor leads to incomplete simplification. Always ensure you find the largest number that divides both the numerator and the denominator without leaving a remainder.
-
Dividing only the numerator or denominator: Remember that to maintain the equivalence of the fraction, both the numerator and the denominator must be divided by the GCD.
-
Not simplifying completely: Ensure that the simplified fraction is in its most reduced form, where the numerator and denominator have no common factors other than 1.
Conclusion: Mastering Fractions for a Stronger Mathematical Foundation
The question "Is 6/8 equal to 3/4?" is a gateway to understanding fundamental concepts in fraction simplification. By mastering the techniques of finding the greatest common divisor and applying the principles of equivalent fractions, you build a stronger foundation for more advanced mathematical concepts and applications. The ability to simplify fractions seamlessly translates to improved problem-solving skills and a more confident approach to mathematical challenges. Remember to practice regularly and use visual aids to enhance your understanding. This will not only help you answer the question "Is 6/8 equal to 3/4?" with certainty, but also empower you to tackle more complex fractional problems with ease and accuracy. The seemingly simple question about the equality of 6/8 and 3/4 opens doors to a deeper understanding of the world of fractions and their crucial role in various mathematical domains.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 6 8 Equal To 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.