Is 6 8 Equivalent To 3 4
News Co
Apr 18, 2025 · 5 min read
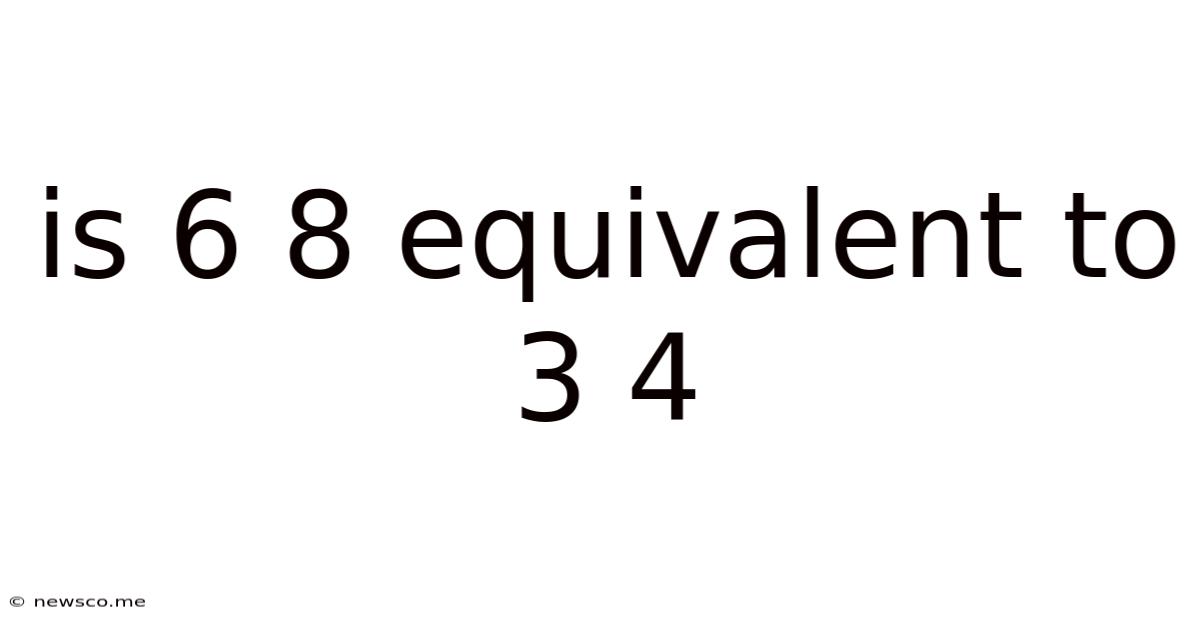
Table of Contents
Is 6:8 Equivalent to 3:4? A Deep Dive into Ratio Equivalence
The question, "Is 6:8 equivalent to 3:4?" seems simple at first glance. However, understanding the concept of ratio equivalence goes beyond a simple "yes" or "no." It delves into the fundamental principles of fractions, proportions, and their applications in various fields. This comprehensive guide will not only answer the question directly but also explore the underlying mathematical concepts, practical applications, and methods for determining ratio equivalence.
Understanding Ratios and Proportions
Before we tackle the specific question, let's establish a solid foundation. A ratio is a comparison of two or more quantities. It expresses the relative sizes of the quantities. We often represent ratios using a colon (e.g., 6:8) or as a fraction (e.g., 6/8).
A proportion is a statement that equates two ratios. It asserts that two ratios are equivalent. For example, 6/8 = 3/4 is a proportion. This statement means that the ratio 6:8 is equivalent to the ratio 3:4.
Determining Ratio Equivalence: The Fundamental Method
The most fundamental method for determining whether two ratios are equivalent is to simplify them to their simplest form. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Let's apply this to our example:
- Ratio 1: 6:8
The GCD of 6 and 8 is 2. Dividing both by 2, we get:
6 ÷ 2 = 3 8 ÷ 2 = 4
Therefore, the simplified form of 6:8 is 3:4.
- Ratio 2: 3:4
This ratio is already in its simplest form because the GCD of 3 and 4 is 1.
Conclusion: Since both ratios simplify to 3:4, we can definitively say that yes, 6:8 is equivalent to 3:4.
Beyond Simplification: Cross-Multiplication
Another powerful technique for verifying ratio equivalence is cross-multiplication. If two ratios are equivalent, the product of their cross-terms will be equal.
Let's illustrate this with our example:
6/8 = 3/4
Cross-multiplying, we get:
6 * 4 = 24 8 * 3 = 24
Since both products are equal, this confirms that the ratios are equivalent.
This method is particularly useful when dealing with larger numbers or ratios that are not easily simplified.
Real-World Applications of Ratio Equivalence
The concept of ratio equivalence is not confined to the realm of theoretical mathematics. It has extensive practical applications in various fields:
1. Cooking and Baking:
Recipes often provide ratios of ingredients. Understanding ratio equivalence allows you to scale recipes up or down while maintaining the same taste and consistency. For instance, if a recipe calls for a 2:1 ratio of flour to sugar, you can use equivalent ratios like 4:2, 6:3, or 8:4 to make larger or smaller batches.
2. Scaling Drawings and Models:
Architects, engineers, and designers use ratios extensively when creating blueprints, models, and scale drawings. Maintaining equivalent ratios ensures accurate representation of real-world objects. A 1:100 scale model means that every 1 unit in the model represents 100 units in the actual object.
3. Mapmaking:
Maps utilize ratios (scales) to represent geographical areas. A map scale might be 1:50,000, meaning 1 cm on the map represents 50,000 cm (or 500 meters) on the ground. Understanding equivalent ratios allows for accurate distance calculations on maps.
4. Finance and Economics:
Ratios are crucial in financial analysis. For example, the debt-to-equity ratio compares a company's debt to its equity. Analyzing equivalent ratios across different companies allows for comparative assessments. Similarly, economic indicators frequently involve ratios comparing various economic factors.
5. Science and Engineering:
Many scientific and engineering principles rely on ratios and proportions. For example, in chemistry, stoichiometry involves calculating the relative amounts of reactants and products in chemical reactions using molar ratios. In physics, ratios are used extensively in calculations involving forces, velocities, and accelerations.
Understanding Non-Equivalent Ratios
It’s equally important to understand how to identify non-equivalent ratios. If, after simplification or cross-multiplication, the ratios are not equal, they are not equivalent.
For example, let's consider the ratios 2:3 and 4:5.
- Simplification: Both ratios are already in their simplest form.
- Cross-multiplication: 2 * 5 = 10 3 * 4 = 12 Since 10 ≠ 12, the ratios 2:3 and 4:5 are not equivalent.
Advanced Concepts: Continued Ratios and Compound Ratios
While the basic understanding of ratio equivalence is crucial, let's briefly touch upon more advanced concepts.
Continued Ratios involve comparing more than two quantities. For example, a continued ratio of 2:3:5 means the quantities are in the ratio of 2:3, 3:5, and 2:5.
Compound Ratios are formed by multiplying the corresponding terms of two or more ratios. For instance, the compound ratio of 2:3 and 4:5 is (24):(35) = 8:15.
Practical Tips for Working with Ratios
- Always simplify ratios to their lowest terms: This makes comparisons and calculations much easier.
- Master cross-multiplication: This technique is a powerful tool for verifying equivalence, particularly with larger numbers.
- Practice regularly: The more you work with ratios, the more comfortable you'll become with understanding and applying their principles.
- Visual aids: Diagrams, charts, and graphs can be helpful in understanding and illustrating ratio relationships.
Conclusion: The Importance of Ratio Equivalence
The ability to determine ratio equivalence is a fundamental mathematical skill with far-reaching applications. From everyday tasks like cooking to complex scientific calculations, understanding how to identify and utilize equivalent ratios is essential for accuracy and efficiency. By mastering the techniques discussed in this article, you'll be well-equipped to tackle any ratio-related problem with confidence. Remember, understanding the "why" behind the mathematical procedures enhances your overall comprehension and problem-solving abilities. The seemingly simple question, "Is 6:8 equivalent to 3:4?", opens a door to a vast world of mathematical concepts and their practical implications.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 6 8 Equivalent To 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.