Is 6 8 Equivalent To 9 12
News Co
Mar 22, 2025 · 5 min read
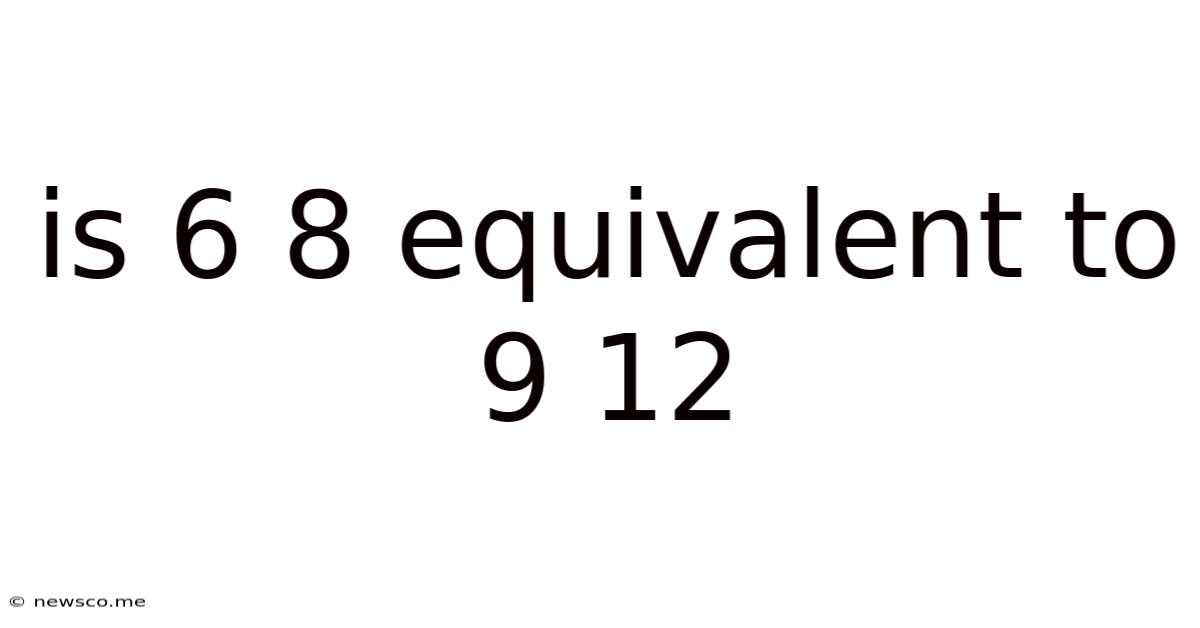
Table of Contents
Is 6:8 Equivalent to 9:12? A Deep Dive into Ratio and Proportion
The question, "Is 6:8 equivalent to 9:12?" might seem simple at first glance. It touches upon fundamental mathematical concepts of ratio and proportion, concepts crucial for understanding various aspects of mathematics, science, and everyday life. This article delves into a comprehensive explanation of ratios, proportions, simplification, and how to determine if two ratios are indeed equivalent. We'll explore different methods and provide numerous examples to solidify your understanding.
Understanding Ratios
A ratio is a comparison of two or more quantities. It shows the relative sizes of the quantities. Ratios can be expressed in several ways:
- Using a colon: 6:8 (read as "6 to 8")
- Using the word "to": 6 to 8
- As a fraction: 6/8
In the ratio 6:8, 6 is the antecedent and 8 is the consequent. The ratio expresses the relationship between the antecedent and the consequent.
Types of Ratios
Ratios can be categorized into different types based on their context and application:
- Part-to-part ratio: This compares one part of a whole to another part of the same whole. For example, in a class with 12 boys and 18 girls, the part-to-part ratio of boys to girls is 12:18.
- Part-to-whole ratio: This compares one part of a whole to the entire whole. For example, in the same class, the part-to-whole ratio of boys to the total number of students is 12:30.
- Ratio of rates: This compares two different rates, such as speed or price. For example, comparing the speed of two cars, one travelling at 60 miles per hour and another at 75 miles per hour, gives a ratio of 60:75.
Understanding Proportions
A proportion is a statement that two ratios are equal. It's an equation where two ratios are set equal to each other. For example, if we have two ratios, a:b and c:d, a proportion would be written as:
a/b = c/d or a:b :: c:d
In this proportion, 'a' and 'd' are called the extremes, and 'b' and 'c' are called the means. A fundamental property of proportions is that the product of the means equals the product of the extremes. This means:
a * d = b * c
This property is incredibly useful for solving problems involving proportions.
Simplifying Ratios
Before comparing ratios, it's often helpful to simplify them to their lowest terms. This is done by finding the greatest common divisor (GCD) of the antecedent and the consequent and dividing both by the GCD.
Let's take the ratio 6:8. The GCD of 6 and 8 is 2. Dividing both by 2, we get:
6/2 : 8/2 = 3:4
The simplified ratio is 3:4. This doesn't change the relationship between the quantities; it just represents them in a more concise form.
Determining Equivalence: 6:8 and 9:12
Now, let's address the original question: Is 6:8 equivalent to 9:12?
We can use several methods to determine this:
Method 1: Simplifying Both Ratios
- Simplify 6:8: The GCD of 6 and 8 is 2. 6:8 simplifies to 3:4.
- Simplify 9:12: The GCD of 9 and 12 is 3. 9:12 simplifies to 3:4.
Since both ratios simplify to 3:4, they are equivalent.
Method 2: Cross-Multiplication
This method utilizes the property of proportions mentioned earlier. If the product of the means equals the product of the extremes, the ratios are equivalent.
6:8 = 9:12
Cross-multiply:
6 * 12 = 72 8 * 9 = 72
Since both products are equal (72 = 72), the ratios 6:8 and 9:12 are equivalent.
Method 3: Dividing to Find the Scaling Factor
We can determine if ratios are equivalent by finding the scaling factor between the corresponding terms.
To go from 6 to 9, we multiply by 1.5 (9/6 = 1.5). To go from 8 to 12, we also multiply by 1.5 (12/8 = 1.5).
Since the same scaling factor applies to both the antecedent and consequent, the ratios are equivalent.
Real-World Applications of Ratios and Proportions
Ratios and proportions are not just abstract mathematical concepts; they have numerous practical applications in various fields:
- Scaling and Drawings: Architects and engineers use ratios and proportions to create scaled drawings of buildings and structures.
- Cooking and Baking: Recipes often involve ratios of ingredients, requiring adjustments based on the number of servings.
- Mixing Paints and Chemicals: Precise ratios are crucial for achieving desired colors or chemical reactions.
- Finance and Investments: Ratios are used extensively in financial analysis to assess the financial health of companies.
- Mapmaking: Maps use scales represented as ratios to accurately depict geographical areas.
Advanced Concepts Related to Ratios and Proportions
While the question of whether 6:8 is equivalent to 9:12 is straightforward, understanding ratios and proportions opens doors to more advanced mathematical concepts:
- Direct Proportion: Two quantities are directly proportional if an increase in one quantity leads to a proportional increase in the other quantity (and vice-versa). For example, the distance traveled is directly proportional to the speed if the time is constant.
- Inverse Proportion: Two quantities are inversely proportional if an increase in one quantity leads to a proportional decrease in the other quantity (and vice-versa). For example, the time taken to complete a task is inversely proportional to the number of workers if the work is constant.
- Continued Proportion: This involves more than two ratios being equal, creating a chain of equivalent ratios.
- Golden Ratio: This is a special irrational number approximately equal to 1.618, which appears frequently in nature, art, and architecture.
Conclusion
The ratios 6:8 and 9:12 are indeed equivalent. Understanding how to determine the equivalence of ratios is essential for various mathematical and real-world applications. By mastering the concepts of ratio, proportion, and simplification, you'll equip yourself with valuable tools for solving problems in numerous fields. Remember to utilize the different methods described above to verify the equivalence of any given ratios, solidifying your understanding and building confidence in your mathematical abilities. Furthermore, exploring advanced concepts like direct and inverse proportions will enhance your understanding of how these fundamental mathematical concepts interact and influence different aspects of the world around us.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 6 8 Equivalent To 9 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.