Is 7 12 Greater Than 1 2
News Co
May 08, 2025 · 5 min read
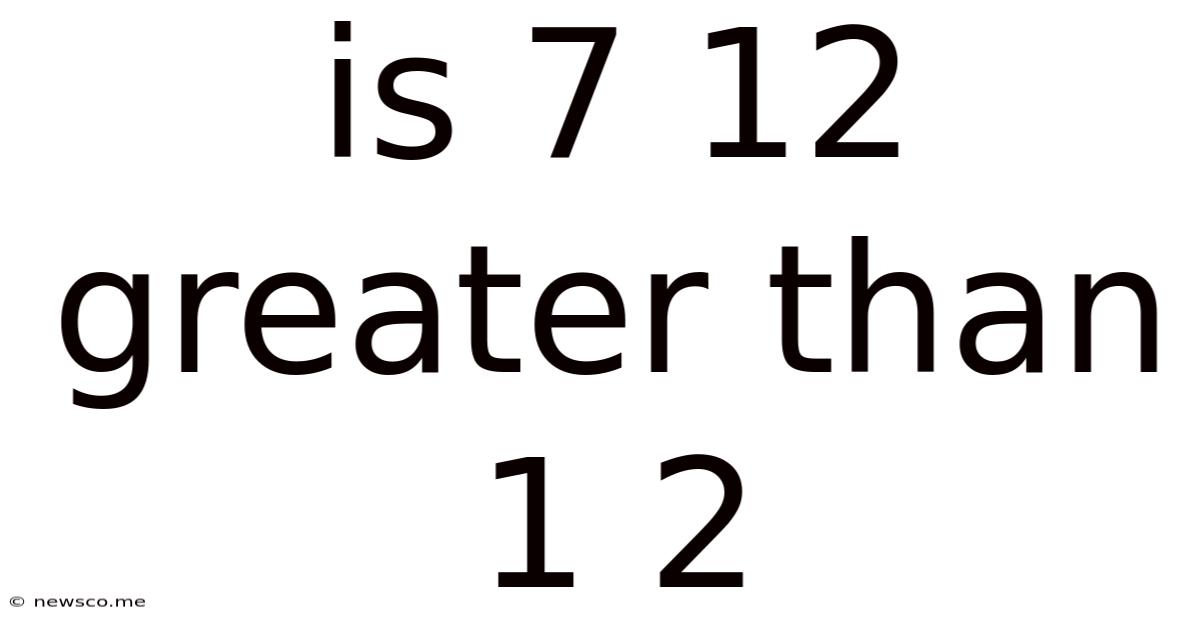
Table of Contents
Is 7/12 Greater Than 1/2? A Deep Dive into Fraction Comparison
Determining whether 7/12 is greater than 1/2 might seem like a simple task, especially for those comfortable with fractions. However, a thorough understanding of this comparison opens the door to a broader comprehension of fraction manipulation and its applications in various fields. This article will not only answer the question definitively but also explore multiple methods to solve such problems, emphasizing the importance of conceptual understanding alongside procedural skills. We'll delve into the nuances of comparing fractions, providing you with a robust toolkit to tackle similar problems with confidence.
Understanding Fractions: A Refresher
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
For instance, in the fraction 7/12, the denominator (12) tells us the whole is divided into 12 equal parts. The numerator (7) indicates we are considering 7 of those 12 parts. Similarly, in 1/2, the whole is divided into two equal parts, and we're considering one of them.
Method 1: Finding a Common Denominator
This is a classic and reliable method for comparing fractions. The core principle is to rewrite both fractions with the same denominator. This allows for a direct comparison of the numerators.
To find a common denominator for 7/12 and 1/2, we need to find a number that is a multiple of both 12 and 2. The least common multiple (LCM) is the smallest such number. In this case, the LCM of 12 and 2 is 12.
- Converting 1/2: To change the denominator of 1/2 to 12, we multiply both the numerator and the denominator by 6 (because 12 ÷ 2 = 6): (1 × 6) / (2 × 6) = 6/12
Now we can compare:
- 7/12 vs 6/12
Since 7 > 6, we conclude that 7/12 > 1/2.
Method 2: Converting to Decimals
Another effective method involves converting both fractions into decimals. This approach is particularly helpful when dealing with more complex fractions or when a decimal representation is more intuitive for comparison.
-
Converting 7/12 to a decimal: Divide 7 by 12: 7 ÷ 12 ≈ 0.5833
-
Converting 1/2 to a decimal: Divide 1 by 2: 1 ÷ 2 = 0.5
Comparing the decimal values: 0.5833 > 0.5, confirming that 7/12 > 1/2.
This method offers a clear visual comparison and is readily adaptable to calculations using a calculator.
Method 3: Visual Representation
For a more intuitive understanding, especially for beginners, visualizing the fractions can be incredibly helpful. Imagine a pizza cut into 12 slices. 7/12 represents having 7 slices, while 1/2 represents having half the pizza, which is 6 slices (12/2 = 6). Clearly, 7 slices are more than 6 slices.
This visual approach reinforces the concept of fractions and makes the comparison easier to grasp. You can use similar visual aids with other shapes or objects to represent fractions and compare them effectively.
Method 4: Using Benchmark Fractions
Benchmark fractions, such as 1/2, 1/4, 3/4, and 1, are useful reference points for estimating the value of other fractions. By comparing the fraction in question to these benchmarks, we can often quickly determine its relative size.
In this case, we can see that 7/12 is slightly more than half (1/2 or 6/12). This quick estimation helps confirm our conclusion that 7/12 > 1/2. This method is useful for mental math and quick comparisons.
Applications of Fraction Comparison
The ability to compare fractions efficiently is not just an academic exercise. It has far-reaching applications in various fields, including:
-
Cooking and Baking: Recipes often require precise measurements, and understanding fractions is crucial for adjusting quantities accurately. Comparing fractions ensures you use the correct amount of ingredients.
-
Construction and Engineering: Many construction projects rely on precise measurements and calculations involving fractions. Accurate fraction comparison is essential for ensuring structural integrity and safety.
-
Finance and Budgeting: Understanding fractions is vital for managing personal finances. Calculating percentages, interest rates, and proportions often involves manipulating and comparing fractions.
-
Data Analysis and Statistics: Many statistical analyses involve working with fractions and proportions. Accurate comparison of fractions is essential for drawing meaningful conclusions from data.
-
Everyday Life: Numerous daily activities involve fractions, such as sharing items fairly, measuring ingredients, and understanding proportions in various contexts.
Advanced Concepts and Further Exploration
Beyond the basic methods discussed above, more advanced techniques exist for comparing fractions, particularly when dealing with more complex fractions or a large number of fractions. These include:
-
Cross-Multiplication: This method is particularly useful for comparing two fractions without finding a common denominator. It involves multiplying the numerator of one fraction by the denominator of the other and vice-versa. The larger product corresponds to the larger fraction.
-
Using Number Lines: Representing fractions on a number line can provide a visual comparison and aid in understanding their relative positions.
-
Converting to Percentages: Converting fractions to percentages provides another method for comparing their relative sizes.
Conclusion: Mastering Fraction Comparison
The simple question, "Is 7/12 greater than 1/2?" serves as a gateway to a much broader understanding of fraction manipulation and its importance in numerous practical applications. By mastering various methods—finding common denominators, converting to decimals, visualizing fractions, and using benchmark fractions—you equip yourself with the tools to confidently and efficiently compare fractions in any context. The ability to compare fractions accurately is not merely a mathematical skill; it's a valuable asset applicable across diverse fields, enhancing problem-solving abilities and promoting a deeper understanding of numerical relationships. Remember to practice regularly and explore the advanced techniques mentioned to further solidify your understanding of this fundamental concept.
Latest Posts
Latest Posts
-
What Do Two Lines Mean In Math
May 08, 2025
-
Adding Integers With The Same Sign Worksheet
May 08, 2025
-
Area And Perimeter Of A Triangle Worksheet
May 08, 2025
-
40 Bottles Of Water Is How Many Gallons
May 08, 2025
-
What Is 72 Written As A Decimal
May 08, 2025
Related Post
Thank you for visiting our website which covers about Is 7 12 Greater Than 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.