Is 7 8 The Same As 3 4
News Co
Apr 20, 2025 · 5 min read
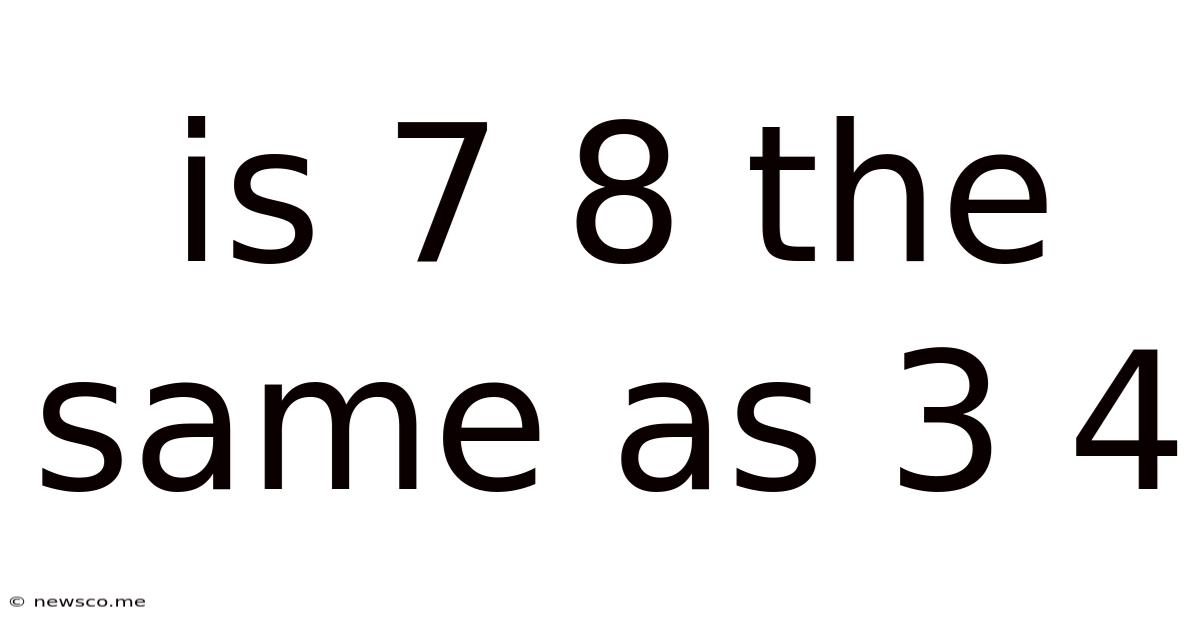
Table of Contents
Is 7/8 the Same as 3/4? A Deep Dive into Fraction Equivalence
Are 7/8 and 3/4 the same? At first glance, they appear different. However, understanding fraction equivalence requires delving into the fundamental concepts of fractions and their representation. This comprehensive guide will explore the relationship between 7/8 and 3/4, explaining why they are not equal, while simultaneously exploring the broader topic of equivalent fractions and how to identify them. We'll also discuss practical applications and problem-solving strategies.
Understanding Fractions: Numerator and Denominator
Before we tackle the core question, let's establish a firm understanding of fractions. A fraction represents a part of a whole. It consists of two key components:
- Numerator: The top number indicates how many parts we have.
- Denominator: The bottom number indicates how many equal parts the whole is divided into.
For example, in the fraction 7/8, the numerator (7) tells us we have seven parts, and the denominator (8) tells us the whole is divided into eight equal parts.
Comparing Fractions: Different Denominators
Comparing fractions with different denominators, like 7/8 and 3/4, requires a common ground. We cannot directly compare them unless they share the same denominator. This necessitates finding equivalent fractions.
Equivalent Fractions: The Concept of Simplification and Expansion
Equivalent fractions represent the same portion of a whole, even though they appear different. Consider a pizza cut into 8 slices. Eating 4 slices is the same as eating half the pizza. Therefore, 4/8 is equivalent to 1/2. We can achieve this equivalence through:
-
Simplification: Reducing a fraction to its simplest form by dividing both the numerator and denominator by their greatest common divisor (GCD). For example, simplifying 4/8 involves dividing both 4 and 8 by their GCD, which is 4, resulting in 1/2.
-
Expansion: Increasing the numerator and denominator by multiplying both by the same number. This doesn't change the fraction's value; it simply represents the same portion with more parts. For example, multiplying both the numerator and denominator of 1/2 by 4 yields 4/8.
Finding a Common Denominator for 7/8 and 3/4
To determine if 7/8 and 3/4 are equal, we need to find a common denominator. This is a number that is a multiple of both denominators (8 and 4). The least common multiple (LCM) of 8 and 4 is 8.
Therefore, we'll convert 3/4 to an equivalent fraction with a denominator of 8:
We multiply both the numerator and denominator of 3/4 by 2:
(3 x 2) / (4 x 2) = 6/8
Now we can compare 7/8 and 6/8. Are they the same?
No, 7/8 is greater than 6/8. Therefore, 7/8 is not the same as 3/4.
Visual Representation: Understanding the Difference
Imagine two identical pizzas. One is cut into 8 equal slices, and the other into 4 equal slices.
-
7/8: You eat 7 out of 8 slices of the first pizza. There's only one slice left.
-
3/4: You eat 3 out of 4 slices of the second pizza. There's one slice left.
While both leave one slice uneaten, the sizes of those remaining slices are different because the pizzas are divided into a different number of pieces. This visual representation clarifies why 7/8 and 3/4 are not equivalent.
Practical Applications: Real-World Examples
The concept of fraction equivalence has numerous real-world applications:
-
Cooking: Recipes often require fractional amounts of ingredients. Understanding equivalent fractions helps adjust recipes for different serving sizes.
-
Construction: Accurate measurements are crucial. Converting between fractions ensures precision in building and other construction projects.
-
Finance: Working with percentages and proportions in budgeting, investments, and financial planning relies heavily on fraction equivalence.
-
Data Analysis: In data representation and statistical analysis, equivalent fractions facilitate comparisons and interpretations of different data sets.
Problem-Solving Strategies: Working with Fractions
When working with fractions, remember these strategies:
-
Find a Common Denominator: This is the cornerstone of comparing and adding/subtracting fractions.
-
Simplify Fractions: Always reduce fractions to their simplest form to avoid unnecessary complexity.
-
Visual Aids: Use diagrams, models, or real-world examples to visualize the fractions and enhance understanding.
-
Cross-Multiplication: This method helps compare two fractions quickly. If a/b and c/d are two fractions, cross-multiply to compare: a x d and b x c. If ad > bc, then a/b > c/d.
Advanced Concepts: Decimals and Percentages
Fractions, decimals, and percentages are all different ways to express parts of a whole. Understanding their interrelationships is essential.
You can convert a fraction to a decimal by dividing the numerator by the denominator.
7/8 = 0.875 3/4 = 0.75
And you can convert fractions to percentages by multiplying the decimal equivalent by 100.
7/8 = 87.5% 3/4 = 75%
These decimal and percentage representations further illustrate that 7/8 and 3/4 are not equivalent.
Conclusion: 7/8 ≠ 3/4
In conclusion, 7/8 and 3/4 are not the same. Although seemingly similar, their fractional representation, visual interpretation, and numerical conversions clearly demonstrate their inequality. A thorough grasp of fraction equivalence, simplification, and the ability to find common denominators is fundamental to accurate mathematical calculations and problem-solving in various real-world contexts. Mastering these concepts will empower you to navigate fractions with confidence and precision. Understanding equivalent fractions is not just about math; it's about developing a deeper understanding of numerical relationships and their practical applications in everyday life.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 7 8 The Same As 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.