Is 8 10 Equivalent To 4 5
News Co
Mar 27, 2025 · 5 min read
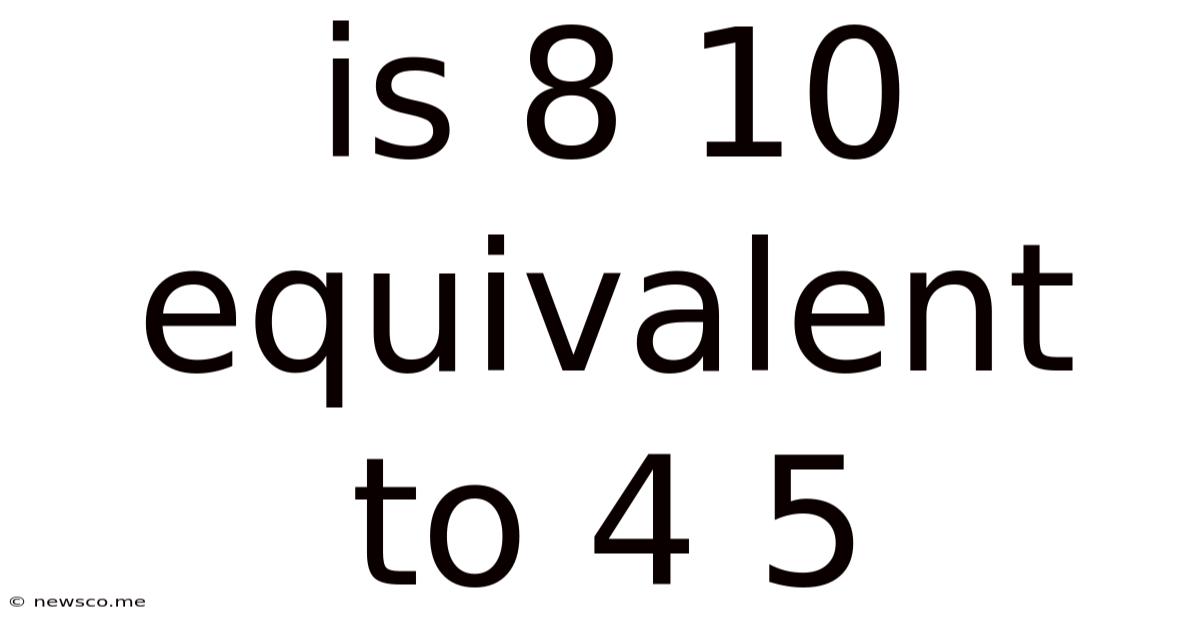
Table of Contents
Is 8:10 Equivalent to 4:5? Understanding Ratios and Proportions
The question, "Is 8:10 equivalent to 4:5?" delves into the fundamental concepts of ratios and proportions. While seemingly simple, understanding the nuances of ratio equivalence is crucial in various fields, from cooking and construction to advanced mathematics and scientific research. This article will thoroughly explore the equivalence of these ratios, explain the underlying mathematical principles, and provide practical examples to solidify your understanding.
What are Ratios and Proportions?
Before diving into the equivalence of 8:10 and 4:5, let's define the core terms:
Ratio: A ratio is a comparison of two or more quantities. It shows the relative sizes of the quantities. Ratios can be expressed in several ways:
- Using a colon: 8:10 (read as "8 to 10")
- As a fraction: 8/10
- Using the word "to": 8 to 10
Proportion: A proportion is a statement that two ratios are equal. It's an equation where two ratios are set equal to each other. For example, 8/10 = 4/5 is a proportion.
Determining Ratio Equivalence: The Fundamentals
To determine if two ratios are equivalent, we need to check if they represent the same relative relationship between the quantities. There are several ways to do this:
1. Simplifying Ratios: The simplest method involves simplifying each ratio to its lowest terms. This is done by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Let's simplify 8:10:
- The GCD of 8 and 10 is 2.
- Dividing both by 2, we get 4:5.
Now, let's compare this simplified ratio to the second ratio, 4:5. Since both ratios, when simplified, are 4:5, they are equivalent.
2. Cross-Multiplication: Another method to check for equivalence is cross-multiplication. If two ratios are equal, the product of the numerator of the first ratio and the denominator of the second ratio will equal the product of the denominator of the first ratio and the numerator of the second ratio.
Let's apply this to 8:10 and 4:5:
- 8/10 = 4/5
- Cross-multiply: (8 * 5) = (10 * 4)
- 40 = 40
Since the cross-products are equal, the ratios are equivalent.
Practical Applications of Ratio Equivalence
Understanding ratio equivalence has numerous practical applications across diverse fields:
1. Cooking and Baking: Recipes often use ratios to specify ingredient proportions. If you need to double or halve a recipe, you must ensure you maintain the correct ratio between ingredients. For example, if a recipe calls for a 2:1 ratio of flour to sugar, doubling the recipe would require a 4:2 ratio, maintaining the same relative proportions.
2. Construction and Engineering: In construction, blueprints rely heavily on ratios and proportions to accurately scale down designs. Ensuring the correct proportions is critical for structural integrity and functionality.
3. Mapmaking and Scaling: Maps use ratios (scales) to represent distances on the earth's surface. A map scale of 1:100,000 means that one unit on the map represents 100,000 units on the ground. Understanding these ratios is essential for accurately interpreting distances and locations.
4. Finance and Economics: Ratios are extensively used in financial analysis to assess the financial health of companies. For example, the debt-to-equity ratio compares a company's debt to its equity, providing insights into its financial leverage.
5. Science and Chemistry: In scientific experiments and chemical reactions, maintaining precise ratios of reactants is vital for achieving desired outcomes.
Beyond Simple Ratios: Dealing with Complex Scenarios
While the example of 8:10 and 4:5 involves simple whole numbers, ratio equivalence can become more complex when dealing with decimals, fractions, or larger numbers. The principles remain the same, though the calculations might involve more steps.
Example with Decimals: Is 2.5:5 equivalent to 1:2?
- Simplify 2.5:5 by dividing both by 2.5, resulting in 1:2.
- Therefore, yes, they are equivalent.
Example with Fractions: Is 1/2 : 1 equivalent to 2/4 : 2?
- Simplify 1/2 : 1 by dividing both by 1/2, resulting in 1 : 2.
- Simplify 2/4 : 2 by simplifying the fraction to 1/2 : 2 and then dividing by 1/2, resulting in 1:4.
- Therefore, no, they are not equivalent.
Example with Larger Numbers: Is 120:180 equivalent to 2:3?
- Find the GCD of 120 and 180, which is 60.
- Divide both by 60, resulting in 2:3.
- Therefore, yes, they are equivalent.
Troubleshooting Common Mistakes
When working with ratios and proportions, be mindful of these common errors:
- Incorrect simplification: Ensure you divide both parts of the ratio by the same number, the GCD.
- Mixing units: When comparing quantities with different units (e.g., meters and centimeters), convert them to the same unit before comparing.
- Misinterpreting the order: Remember that the order in which you write the ratio matters. 8:10 is not the same as 10:8.
Conclusion: Mastering Ratios and Proportions
The question of whether 8:10 is equivalent to 4:5 leads us to a deeper understanding of ratios and proportions – fundamental mathematical concepts with far-reaching applications. By mastering these concepts and employing the methods discussed above – simplification and cross-multiplication – you can confidently determine the equivalence of any two ratios, ensuring accuracy and precision in various fields. Remember to practice regularly and pay close attention to detail to avoid common errors. This strong foundation will be invaluable as you progress in your mathematical studies and apply these concepts to real-world problems. The ability to identify equivalent ratios unlocks a deeper understanding of relative sizes and proportions, crucial for success in many areas of life.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 8 10 Equivalent To 4 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.