Is 98 A Prime Or Composite Number
News Co
Apr 26, 2025 · 5 min read
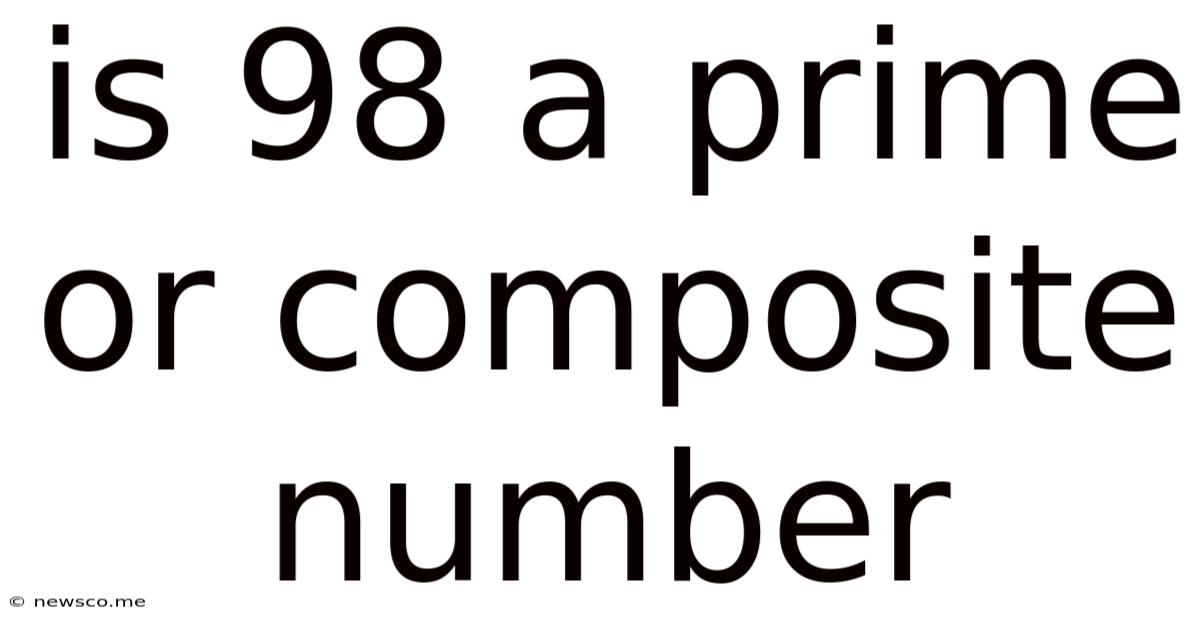
Table of Contents
Is 98 a Prime or Composite Number? A Deep Dive into Number Theory
Determining whether a number is prime or composite is a fundamental concept in number theory. While seemingly simple for smaller numbers, understanding the process and its implications becomes increasingly crucial as numbers grow larger. This article will thoroughly explore whether 98 is a prime or composite number, delving into the definitions, methods for determining primality, and the broader significance of prime and composite numbers in mathematics.
Understanding Prime and Composite Numbers
Before classifying 98, let's clarify the definitions:
Prime Number: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself without leaving a remainder. Examples include 2, 3, 5, 7, 11, and so on.
Composite Number: A composite number is a natural number greater than 1 that is not a prime number. This means it has at least one positive divisor other than 1 and itself. Examples include 4 (2 x 2), 6 (2 x 3), 9 (3 x 3), and countless others.
Neither Prime nor Composite: The numbers 0 and 1 are neither prime nor composite. This is a crucial distinction often overlooked.
Determining if 98 is Prime or Composite
To determine the nature of 98, we can employ several methods:
1. The Trial Division Method
This is the most straightforward approach. We systematically check if 98 is divisible by any integer from 2 up to the square root of 98 (approximately 9.89). If we find a divisor other than 1 and 98, we know it's composite.
Let's try:
- Is 98 divisible by 2? Yes, 98 ÷ 2 = 49.
Since we found a divisor (2) other than 1 and 98, we can definitively conclude that 98 is a composite number. There's no need to check further divisors; finding one is sufficient to classify it as composite.
2. Prime Factorization
Prime factorization involves expressing a number as a product of its prime factors. This method not only confirms whether a number is composite but also reveals its prime constituents.
Let's factorize 98:
98 = 2 x 49
Since 49 is 7 x 7, the complete prime factorization is:
98 = 2 x 7 x 7 or 2 x 7<sup>2</sup>
The presence of factors other than 1 and 98 (namely, 2 and 7) confirms that 98 is a composite number.
3. Recognizing Patterns and Divisibility Rules
Understanding divisibility rules can expedite the process. For instance:
- Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8). Since 98 ends in 8, it's immediately evident that it's divisible by 2.
This quick check, using the divisibility rule for 2, is often the fastest way to determine if a number is composite. If a number isn't divisible by 2, you can proceed to check other divisibility rules (e.g., for 3, 5, 7, 11, etc.).
The Significance of Prime and Composite Numbers
The classification of numbers as prime or composite is far from a mere academic exercise. Prime numbers form the building blocks of all other whole numbers through the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers (ignoring the order of the factors).
This fundamental principle has profound implications across various fields:
1. Cryptography
Prime numbers are the cornerstone of modern cryptography, particularly in public-key cryptography systems like RSA. The security of these systems relies on the difficulty of factoring very large composite numbers into their prime components. The larger the prime numbers used, the more secure the encryption.
2. Number Theory Research
Prime numbers are a central focus of ongoing research in number theory. Unanswered questions, such as the distribution of prime numbers and the Riemann Hypothesis (concerning the distribution of prime numbers), continue to challenge mathematicians worldwide.
3. Computer Science
Prime numbers play a role in various algorithms and data structures in computer science, including hash tables and certain types of data compression.
4. Other Applications
The properties of prime and composite numbers have applications in areas such as:
- Coding Theory: Designing efficient error-correcting codes.
- Physics: Studying patterns in physical phenomena.
- Engineering: Optimizing designs and structures.
Beyond 98: Exploring Larger Numbers
While determining whether 98 is prime or composite is relatively straightforward, the task becomes more computationally intensive for significantly larger numbers. Sophisticated algorithms, such as the Miller-Rabin primality test (a probabilistic test) and the AKS primality test (a deterministic test), are employed to efficiently determine the primality of extremely large numbers, often used in cryptography.
Conclusion: 98 is Definitely Composite
Through various methods, including trial division and prime factorization, we've conclusively established that 98 is a composite number. Its prime factorization (2 x 7 x 7) clearly demonstrates the presence of factors beyond 1 and itself. Understanding the difference between prime and composite numbers is fundamental to appreciating the structure of the number system and its far-reaching applications in diverse fields. The seemingly simple question of whether 98 is prime or composite opens the door to a vast and fascinating world of mathematical concepts and their practical implications. Furthermore, understanding this fundamental concept lays the groundwork for exploring more complex areas within number theory and related fields. The ability to quickly and accurately identify prime and composite numbers is a critical skill for anyone interested in mathematics, computer science, or cryptography.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is 98 A Prime Or Composite Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.