Is A Kite Always A Quadrilateral
News Co
Apr 06, 2025 · 5 min read
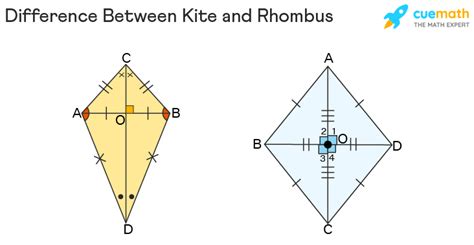
Table of Contents
Is a Kite Always a Quadrilateral? Exploring the Geometry of Kites
The question, "Is a kite always a quadrilateral?" might seem simple at first glance. However, a deeper dive into the geometric properties of kites reveals a more nuanced answer, highlighting the intricate relationships between different shapes and their defining characteristics. This article explores the definition of a kite, its relationship to quadrilaterals, and examines special cases to fully address the question.
Understanding Quadrilaterals: The Broader Family
Before delving into kites, let's establish a firm understanding of quadrilaterals. A quadrilateral is simply any polygon with four sides. This broad category encompasses a vast array of shapes, including squares, rectangles, rhombuses, parallelograms, trapezoids, and of course, kites. The defining characteristic of all quadrilaterals is their four sides and four angles, with the sum of their interior angles always equaling 360 degrees. This fundamental property serves as the foundation for understanding the relationship between quadrilaterals and their specific subtypes, such as kites.
The Diverse Family of Quadrilaterals: A Quick Overview
Let's briefly review some of the key quadrilateral types:
- Parallelogram: A quadrilateral with opposite sides parallel. Rectangles, rhombuses, and squares are all special types of parallelograms.
- Rectangle: A parallelogram with four right angles.
- Rhombus: A parallelogram with four sides of equal length.
- Square: A quadrilateral that is both a rectangle and a rhombus – it possesses four right angles and four equal sides.
- Trapezoid (or Trapezium): A quadrilateral with at least one pair of parallel sides.
- Isosceles Trapezoid: A trapezoid where the non-parallel sides are equal in length.
Defining a Kite: More Than Just a Toy
A kite, in the geometric sense, is a quadrilateral with two pairs of adjacent sides that are equal in length. Think of the classic toy kite: two pairs of sticks forming the frame, with the pairs of equal length joined at a central point. This visual representation helps solidify the understanding of the kite's defining property. Crucially, the pairs of equal sides are adjacent, meaning they share a common vertex (corner). This distinction is essential to differentiate a kite from other quadrilaterals.
Key Properties of a Kite:
- Two pairs of adjacent congruent sides: This is the defining characteristic of a kite.
- One pair of opposite angles are congruent: The angles between the unequal sides are equal.
- Diagonals are perpendicular: The longer diagonal bisects the shorter diagonal.
- Only one diagonal bisects the other: This is a distinguishing feature that separates kites from other quadrilaterals.
Is a Kite Always a Quadrilateral? A Definitive Answer
The answer to the central question is a resounding yes. Because a kite, by definition, has four sides, it unequivocally falls under the umbrella of quadrilaterals. All kites are quadrilaterals, but not all quadrilaterals are kites. This highlights the hierarchical relationship between the broader category of quadrilaterals and its more specific subtype, the kite.
Illustrating the Relationship: Venn Diagram
Imagine a Venn diagram: the larger circle represents all quadrilaterals. Inside this larger circle, a smaller circle represents kites. Every point within the smaller circle (representing a kite) is also within the larger circle (representing quadrilaterals). However, there are many points within the larger circle that are not within the smaller circle – these represent quadrilaterals that are not kites.
Special Cases and Considerations: Are all Kites the Same?
While all kites are quadrilaterals, it's important to recognize that not all kites are created equal. Some kites possess additional properties that elevate them to other more specific quadrilateral classifications.
The Rhombus as a Special Kite:
A rhombus is a quadrilateral with all four sides of equal length. A special type of kite, where all four sides are congruent, is also a rhombus. This highlights the overlap between these two quadrilateral types. In this specific case, the kite satisfies the conditions of a rhombus. It's crucial to remember that a rhombus is a type of parallelogram. So, the particular kite that is also a rhombus is also a parallelogram.
The Square as a Very Special Kite:
Taking it a step further, a square possesses all the properties of a rhombus, including four congruent sides. A square is also a rectangle (four right angles). Therefore, a square can also be considered a special case of a kite where all sides are equal and all angles are right angles. This illustrates the nested nature of these geometric classifications. A square is a kite, a rhombus, a parallelogram, and a rectangle.
Why is Understanding This Important?
Understanding the precise relationship between kites and quadrilaterals is crucial for several reasons:
- Geometric Reasoning: It strengthens foundational geometric understanding, helping to build a solid base for more advanced mathematical concepts.
- Problem-Solving: Recognizing the properties of kites allows for efficient problem-solving in geometry, particularly when dealing with area, perimeter, and angle calculations.
- Spatial Reasoning: It enhances spatial reasoning abilities, allowing for better visualization and interpretation of geometric shapes in two-dimensional space.
Conclusion: Kites are a Unique Family Within the Quadrilateral Clan
In conclusion, the answer to "Is a kite always a quadrilateral?" is definitively yes. Kites, with their unique properties of two pairs of adjacent equal sides, are an important subtype within the larger family of quadrilaterals. Understanding the specific properties of kites and their relationship to other quadrilaterals like rhombuses and squares, strengthens geometric understanding and enhances problem-solving skills. The exploration of these shapes provides a valuable insight into the rich interconnectedness of geometric concepts. Therefore, while seemingly a simple question, understanding the relationships between kites and quadrilaterals unveils a fascinating world of mathematical connections.
Latest Posts
Latest Posts
-
Greatest Common Factor Least Common Multiple Worksheet
Apr 07, 2025
-
How Many Right Angles Does A Rectangle Have
Apr 07, 2025
-
How Many Feet Are In A Tenth Of A Mile
Apr 07, 2025
-
Volume Of A Rectangular Based Pyramid
Apr 07, 2025
-
How Many Vertices Does A Trapezium Have
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Is A Kite Always A Quadrilateral . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
