Is A Rectangle Is A Parallelogram
News Co
Apr 06, 2025 · 5 min read
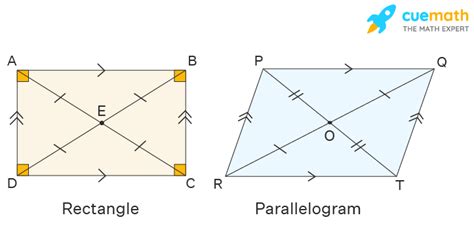
Table of Contents
Is a Rectangle a Parallelogram? A Deep Dive into Quadrilateral Geometry
The question, "Is a rectangle a parallelogram?" might seem simple at first glance. The answer, unequivocally, is yes. However, understanding why requires a deeper exploration into the definitions and properties of parallelograms and rectangles, delving into the fascinating world of quadrilateral geometry. This comprehensive guide will not only answer the question definitively but also explore the broader relationships between various quadrilaterals, enriching your understanding of geometric concepts.
Understanding Parallelograms: The Foundation
Before we can definitively classify a rectangle, we must first solidify our understanding of a parallelogram. A parallelogram is a quadrilateral (a four-sided polygon) with the following defining properties:
- Opposite sides are parallel: This is the core characteristic of a parallelogram. Think of two pairs of parallel lines forming the shape.
- Opposite sides are congruent: The lengths of opposite sides are equal.
- Opposite angles are congruent: The angles opposite each other are equal in measure.
- Consecutive angles are supplementary: The sum of any two adjacent angles is 180 degrees.
- Diagonals bisect each other: The diagonals of a parallelogram intersect at their midpoints.
These properties are interconnected; if you prove one, you can logically deduce the others. This interconnectedness is crucial when classifying quadrilaterals.
Identifying Parallelograms: Practical Examples
Imagine a perfectly aligned window frame, or the opposite sides of a perfectly constructed building. These shapes exemplify the properties of a parallelogram: opposite sides run parallel and are equal in length. Even a tilted, slightly skewed parallelogram still adheres to these fundamental properties, though it might not appear as visually symmetrical as a rectangle.
Delving into Rectangles: A Special Case
A rectangle, on the other hand, is a more specific type of parallelogram with additional properties:
- All four angles are right angles (90 degrees): This is the defining characteristic that distinguishes a rectangle from other parallelograms. The sides meet at perfect right angles.
- Opposite sides are parallel and congruent: This inherits directly from its parallelogram properties.
- Diagonals are congruent: Unlike general parallelograms, the diagonals of a rectangle are equal in length.
- Diagonals bisect each other: This is a property shared with all parallelograms.
Rectangles: A Visual Representation
Think of a standard piece of paper or a computer screen. These are perfect examples of rectangles, highlighting the presence of four right angles and opposite sides that are both parallel and equal in length. The diagonals, when drawn, would be easily seen as equal in length, further emphasizing the unique properties of a rectangle.
Proving the Relationship: Rectangle as a Parallelogram
Since a rectangle possesses all the properties of a parallelogram, it's categorized as a special case or a subclass of a parallelogram. This means every rectangle is a parallelogram, but not every parallelogram is a rectangle. This hierarchical relationship is key to understanding quadrilateral classification.
We can demonstrate this using deductive reasoning:
- Definition of a Rectangle: A rectangle is a quadrilateral with four right angles.
- Properties of a Rectangle: Because of its four right angles, opposite angles are congruent (90 degrees each), and consecutive angles are supplementary (90 + 90 = 180 degrees).
- Parallel Lines and Right Angles: If we have four right angles, the lines forming those angles must be parallel. This stems from basic geometry principles concerning transversal lines and their angles.
- Conclusion: Since a rectangle possesses parallel opposite sides (derived from step 3), it fulfills the defining property of a parallelogram. Therefore, a rectangle is a parallelogram.
This logical progression clearly establishes the relationship. The key is understanding that the defining characteristics of a rectangle automatically imply the defining characteristics of a parallelogram.
The Hierarchy of Quadrilaterals: A Broader Perspective
Understanding the relationship between rectangles and parallelograms necessitates placing them within the broader context of quadrilateral classification. The hierarchy can be visualized as follows:
- Quadrilaterals: The broadest category, encompassing all four-sided polygons.
- Trapezoids: Quadrilaterals with at least one pair of parallel sides.
- Isosceles Trapezoids: Trapezoids with congruent legs.
- Parallelograms: Quadrilaterals with two pairs of parallel sides.
- Rectangles: Parallelograms with four right angles.
- Squares: Rectangles with four congruent sides.
- Rhombuses: Parallelograms with four congruent sides.
- Squares: Rhombuses with four right angles.
- Rectangles: Parallelograms with four right angles.
- Trapezoids: Quadrilaterals with at least one pair of parallel sides.
This hierarchy demonstrates that squares are a special case of both rectangles and rhombuses, illustrating how specific properties lead to increasingly specialized quadrilaterals. Each category inherits properties from its parent category, while adding unique characteristics of its own.
Beyond the Definition: Applications and Significance
Understanding the relationship between rectangles and parallelograms isn't merely an academic exercise; it has significant practical applications:
- Engineering and Construction: Designing structures relies heavily on geometric principles. The properties of parallelograms and rectangles are crucial for ensuring stability and strength in buildings, bridges, and other structures. Understanding their properties allows for precise calculations and effective design.
- Computer Graphics and Design: In computer-aided design (CAD) software and graphics applications, understanding quadrilateral properties is fundamental. Creating and manipulating shapes accurately requires a deep understanding of their geometric relationships.
- Physics and Mathematics: The principles of parallelogram and rectangle geometry are foundational to many areas of physics and mathematics, including vector analysis and coordinate geometry.
Common Misconceptions and Clarifications
It's essential to address common misconceptions that might arise from this discussion:
- Not all parallelograms are rectangles: This is crucial. A parallelogram can have angles other than 90 degrees, while a rectangle must have four 90-degree angles.
- Rectangles are a subset of parallelograms: This highlights the hierarchical relationship, where all rectangles fit into the broader category of parallelograms.
- Properties are inherited, not interchangeable: A rectangle inherits the properties of a parallelogram but adds its own unique characteristics.
Conclusion: A Solid Understanding of Geometric Relationships
In conclusion, the answer to "Is a rectangle a parallelogram?" is a resounding yes. Understanding this relationship requires a firm grasp of the defining properties of both shapes and their hierarchical placement within the broader classification of quadrilaterals. This understanding isn't just about memorizing definitions; it's about appreciating the interconnectedness of geometric concepts and their practical significance across diverse fields. By understanding these relationships, we can better appreciate the elegance and power of geometry in solving real-world problems. The seemingly simple question about rectangles and parallelograms opens a door to a deeper understanding of the world around us, expressed in the language of shapes and angles.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is A Rectangle Is A Parallelogram . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.