Is Square Root Of 121 A Rational Number
News Co
Mar 27, 2025 · 5 min read
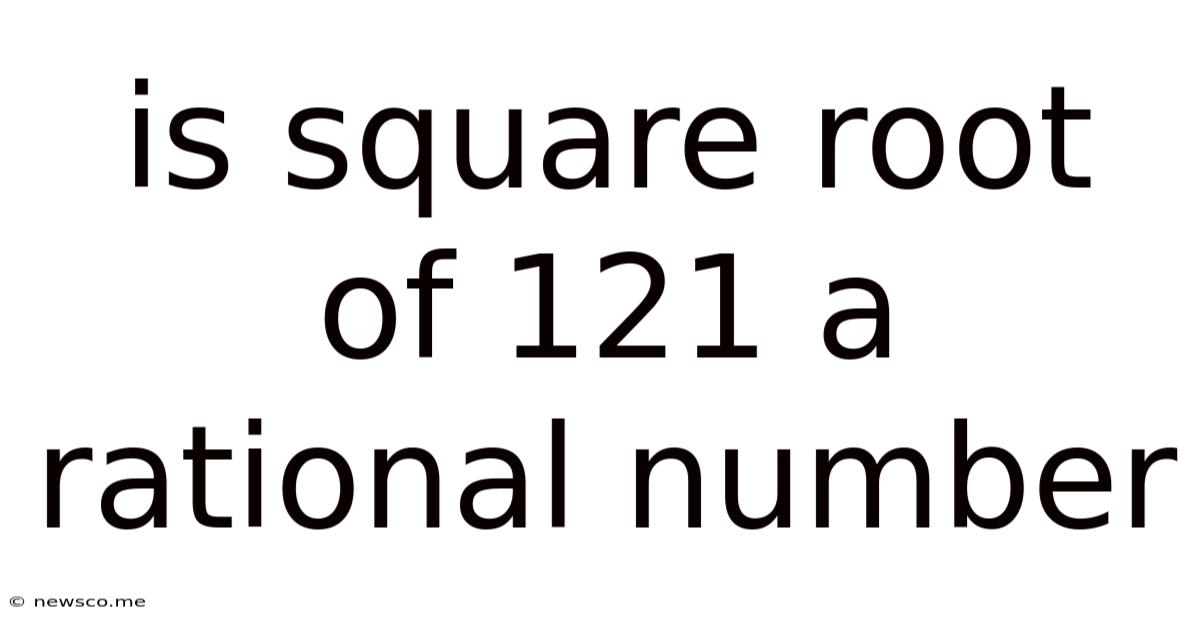
Table of Contents
Is the Square Root of 121 a Rational Number? A Deep Dive into Rationality and Irrationality
The question, "Is the square root of 121 a rational number?" might seem deceptively simple at first glance. However, exploring this question provides a fantastic opportunity to delve into the fundamental concepts of rational and irrational numbers, their properties, and how to definitively classify numbers based on their characteristics. This article will not only answer the question definitively but also explore related concepts to provide a comprehensive understanding of the topic.
Understanding Rational Numbers
Before tackling the square root of 121, let's establish a solid foundation by defining rational numbers. A rational number is any number that can be expressed as a fraction p/q, where:
- p and q are integers (whole numbers, including zero and negative numbers).
- q is not equal to zero (division by zero is undefined).
This definition encompasses a broad range of numbers, including:
- Integers: Whole numbers like -3, 0, 5, 100, etc., can be expressed as fractions (e.g., 5/1, 100/1).
- Fractions: Obvious examples like 1/2, 3/4, -7/8, etc., directly fit the p/q format.
- Terminating Decimals: Decimals that end, such as 0.75 (which is 3/4), 2.5 (which is 5/2), or -0.125 (which is -1/8), can all be converted into fractions.
- Repeating Decimals: Decimals with a pattern that repeats infinitely, like 0.333... (which is 1/3) or 0.142857142857... (which is 1/7), are also rational. There's always a way to express them as a fraction.
Understanding Irrational Numbers
Conversely, irrational numbers cannot be expressed as a fraction p/q, where p and q are integers and q is not zero. Their decimal representation is non-terminating and non-repeating; the digits go on forever without ever falling into a predictable pattern. Famous examples include:
- π (Pi): The ratio of a circle's circumference to its diameter, approximately 3.14159..., continues infinitely without repeating.
- e (Euler's number): The base of natural logarithms, approximately 2.71828..., is also an irrational number.
- √2 (Square root of 2): This number, approximately 1.414213..., cannot be expressed as a simple fraction.
Calculating the Square Root of 121
Now, let's focus on the core question: Is √121 a rational number? To determine this, we need to calculate the square root of 121. The square root of a number is a value that, when multiplied by itself, equals the original number. In this case:
11 x 11 = 121
Therefore, the square root of 121 is 11.
Classifying √121: Rational or Irrational?
Since 11 is an integer, and integers are a subset of rational numbers (remember, any integer can be expressed as a fraction with a denominator of 1; 11 = 11/1), we can definitively conclude that √121 is a rational number.
Further Exploration of Rational and Irrational Numbers
Let's expand our understanding of these number types with some further considerations:
Properties of Rational Numbers
- Closure under addition, subtraction, multiplication, and division: When you add, subtract, multiply, or divide two rational numbers (excluding division by zero), the result is always another rational number.
- Density: Between any two rational numbers, you can always find another rational number. This property implies an infinite number of rational numbers between any two given rational numbers.
- Countability: While there are infinitely many rational numbers, they are "countable," meaning you could theoretically list them in a sequence. This might seem counterintuitive, but mathematical proofs demonstrate this surprising characteristic.
Properties of Irrational Numbers
- Non-closure: Irrational numbers do not exhibit closure under the basic arithmetic operations. For example, the sum of two irrational numbers can be rational (e.g., (√2 + (-√2)) = 0), while the product of two irrational numbers can also be rational (e.g., √2 * √2 = 2).
- Density: Similar to rational numbers, irrational numbers are dense on the number line; you can always find another irrational number between any two given irrational numbers.
- Uncountability: Unlike rational numbers, irrational numbers are "uncountable." There are infinitely more irrational numbers than rational numbers. This is a profound concept in set theory.
Identifying Rational and Irrational Numbers
Here's a practical guide to help you distinguish between rational and irrational numbers:
- Check for fractional representation: If a number can be expressed as a fraction p/q (with integer p and non-zero integer q), it's rational.
- Examine the decimal representation: If the decimal representation terminates (ends) or repeats in a predictable pattern, the number is rational. If it's non-terminating and non-repeating, it's irrational.
- Recognize common irrational numbers: Be aware of well-known irrational numbers like π, e, and square roots of non-perfect squares (e.g., √3, √5, √7).
Real-World Applications of Rational and Irrational Numbers
Rational and irrational numbers are not just abstract mathematical concepts; they have practical applications in various fields:
- Engineering and Physics: Rational numbers are essential for precise measurements and calculations in engineering designs and physical models. Irrational numbers, such as π, are crucial in calculations related to circles, spheres, and other curved shapes.
- Finance: Rational numbers are used extensively in financial calculations, including interest rates, stock prices, and currency conversions.
- Computer Science: Rational numbers are fundamental in computer algorithms and data structures. Representing irrational numbers requires approximation techniques.
- Construction: The concept of rational numbers is paramount in ensuring accurate measurements and calculations for building structures.
Conclusion: The Square Root of 121 is Rational
To reiterate, the square root of 121 is 11, which is an integer and therefore a rational number. Understanding the difference between rational and irrational numbers is crucial for a solid foundation in mathematics and its various applications. This article has explored these concepts in depth, providing a comprehensive explanation and practical guidance for identifying and classifying different types of numbers. Remember that while seemingly simple, the exploration of rational and irrational numbers unveils a rich and fascinating world of mathematical concepts with far-reaching implications. By mastering these fundamentals, you'll be better equipped to tackle more complex mathematical problems and appreciate the elegance and power of mathematics in various fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is Square Root Of 121 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.