Is Square Root The Same As 1/2 Power
News Co
May 08, 2025 · 5 min read
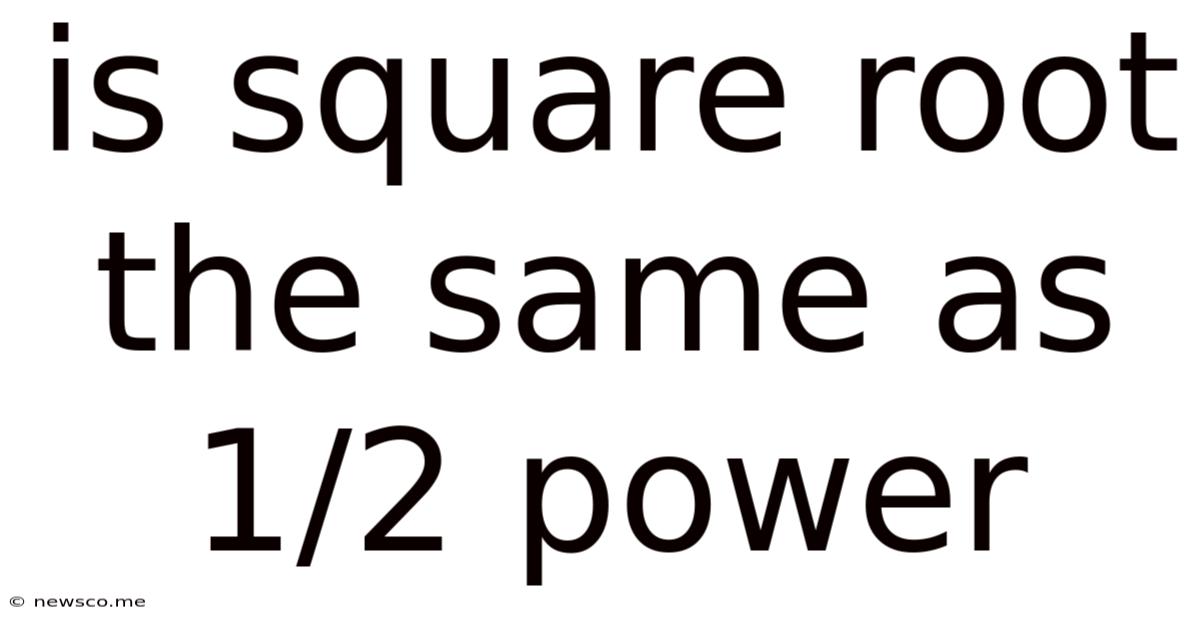
Table of Contents
Is Square Root the Same as 1/2 Power? A Deep Dive into Exponents and Radicals
The question, "Is a square root the same as a 1/2 power?" is a common one among students learning algebra and beyond. The short answer is a resounding yes. However, understanding why this is true requires a deeper exploration of exponents, radicals, and their interconnectedness. This comprehensive guide will unravel the intricacies of this mathematical equivalence, providing a robust understanding for both beginners and those seeking a refresher.
Understanding Exponents: A Foundation
Before diving into the equivalence of square roots and the 1/2 power, let's establish a solid understanding of exponents. Exponents, or indices, represent repeated multiplication. For example:
- x² means x * x (x multiplied by itself twice)
- x³ means x * x * x (x multiplied by itself three times)
- xⁿ means x multiplied by itself 'n' times
This concept readily extends to fractional exponents, which is where the connection to square roots becomes apparent.
Fractional Exponents: Unveiling the Mystery
Fractional exponents represent a combination of exponentiation and root extraction. The general form is:
x<sup>m/n</sup> = (<sup>n</sup>√x)<sup>m</sup>
where:
- m is the power.
- n is the root (e.g., square root, cube root, etc.).
This formula states that raising x to the power of m/n is equivalent to taking the nth root of x and then raising the result to the power of m.
Let's break this down further with some examples.
-
x<sup>1/2</sup>: This represents taking the square root of x. The numerator (1) indicates the power, and the denominator (2) indicates the root (square root). Therefore, x<sup>1/2</sup> = √x.
-
x<sup>1/3</sup>: This represents taking the cube root of x. The numerator is 1 (the power), and the denominator is 3 (the cube root). Therefore, x<sup>1/3</sup> = ³√x.
-
x<sup>2/3</sup>: This represents taking the cube root of x and then squaring the result. It can be written as (³√x)² or (x<sup>1/3</sup>)².
-
x<sup>-1/2</sup>: The negative exponent means taking the reciprocal. This is equivalent to 1/√x or 1/x<sup>1/2</sup>.
The Equivalence: Square Root and 1/2 Power
Now, let's directly address the core question: Why is the square root of a number the same as raising that number to the power of 1/2?
The equivalence stems directly from the definition of fractional exponents. As explained above, x<sup>m/n</sup> = (<sup>n</sup>√x)<sup>m</sup>. If we substitute m = 1 and n = 2, we get:
x<sup>1/2</sup> = (²√x)¹ = √x
This clearly shows that raising a number to the power of 1/2 is precisely the same as taking its square root. This holds true for positive real numbers. For complex numbers, the concept is more nuanced and requires a deeper understanding of complex analysis. We'll focus on the real numbers for this discussion.
Practical Applications and Examples
Understanding the equivalence between square roots and the 1/2 power has significant practical implications in various areas of mathematics and beyond:
1. Simplification of Expressions: The equivalence allows us to simplify complex expressions. For instance, instead of writing √(x²y), we can write (x²y)<sup>1/2</sup>, which can often lead to easier manipulations and simplifications, especially when dealing with more intricate expressions involving multiple roots and powers.
2. Solving Equations: This equivalence is crucial when solving equations involving square roots. For example, consider the equation √x = 5. By rewriting this as x<sup>1/2</sup> = 5, we can easily solve for x by squaring both sides: (x<sup>1/2</sup>)² = 5², which simplifies to x = 25.
3. Calculus and Advanced Mathematics: The 1/2 power representation becomes particularly important in calculus and other advanced mathematical fields. Derivatives and integrals often involve fractional exponents, making the equivalence invaluable for manipulating and solving problems. For instance, the derivative of x<sup>1/2</sup> is easily computed using the power rule.
4. Programming and Computational Applications: Many programming languages and software applications use the 1/2 power notation for square roots, primarily because it's more computationally efficient in various algorithms.
Addressing Potential Confusion and Caveats
While the equivalence is generally true, it's essential to acknowledge some subtleties:
1. Negative Numbers: When dealing with even roots (such as square roots), taking the root of a negative number involves complex numbers. While we can write (-9)<sup>1/2</sup>, the result is a complex number (3i, where 'i' is the imaginary unit). It's crucial to remember that the principal square root of a negative number is a complex number.
2. Order of Operations: Remember to follow the order of operations (PEMDAS/BODMAS) when evaluating expressions. Exponents should be evaluated before multiplication or division. For example, 2 * x<sup>1/2</sup> is different from (2x)<sup>1/2</sup>.
3. Mathematical Notation: Although mathematically equivalent, the square root symbol (√) and the fractional exponent notation (<sup>1/2</sup>) sometimes convey slightly different implications in certain contexts. For example, the square root symbol often implies the principal square root only, while the fractional exponent notation could encompass both the positive and negative square root in some contexts. This distinction might be important in higher-level mathematics.
Conclusion: Mastering the Interplay of Exponents and Radicals
The equivalence between the square root and the 1/2 power is a fundamental concept in mathematics with far-reaching implications. By understanding this equivalence, we can simplify expressions, solve equations, and tackle more complex problems involving exponents and radicals with greater ease and confidence. The key is to grasp the underlying principles of fractional exponents and to be mindful of the subtleties when working with negative numbers and complex numbers. This thorough understanding builds a strong foundation for more advanced mathematical studies and applications. Remember, the seemingly simple relationship between square roots and the 1/2 power is a cornerstone of mathematical elegance and efficiency.
Latest Posts
Latest Posts
-
Area Of Circle Inside A Square
May 08, 2025
-
How Many Liters Are In 1 Quart
May 08, 2025
-
What Fractions Are Equal To 1 5
May 08, 2025
-
Is 3 A Rational Number Yes Or No
May 08, 2025
-
Equilateral Triangle Inscribed In A Circle Formula
May 08, 2025
Related Post
Thank you for visiting our website which covers about Is Square Root The Same As 1/2 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.