Is The Quotient Of Two Rational Numbers Always Rational
News Co
Apr 27, 2025 · 4 min read
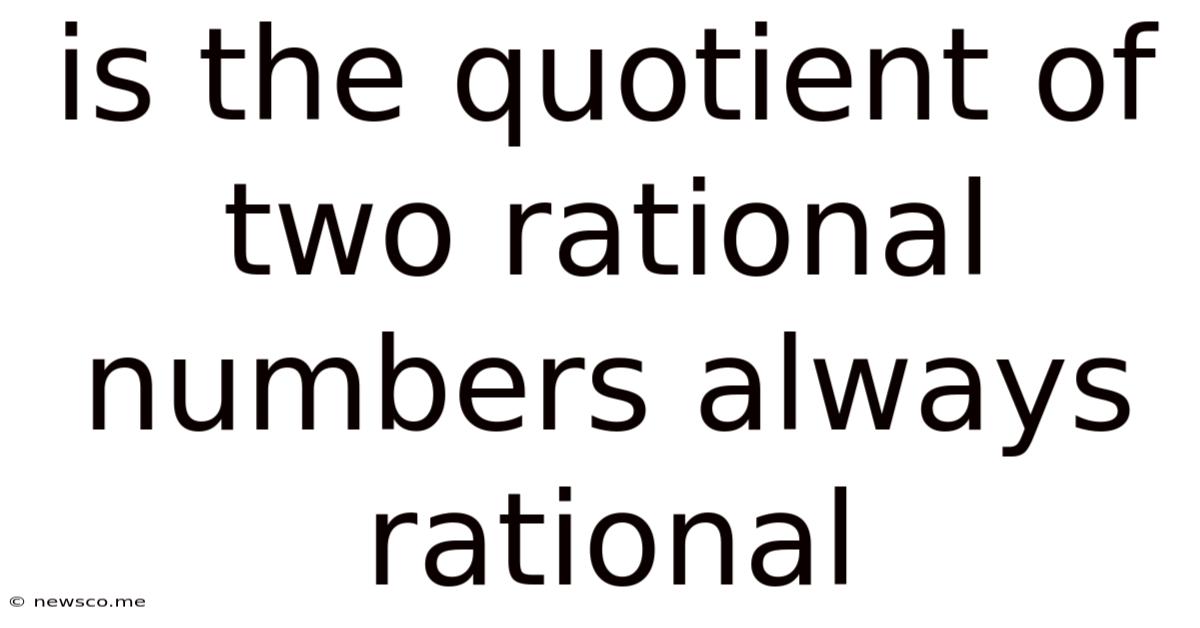
Table of Contents
Is the Quotient of Two Rational Numbers Always Rational? A Deep Dive into Rational Numbers and Their Properties
The question of whether the quotient of two rational numbers is always rational is a fundamental concept in mathematics, particularly within the realm of number theory. The short answer is a resounding yes, but understanding why requires a deeper exploration of rational numbers, their properties, and the operations performed on them. This article will delve into this topic, providing a comprehensive explanation supported by examples and addressing potential exceptions or nuances.
Understanding Rational Numbers
Before we tackle the central question, let's establish a firm understanding of what constitutes a rational number. A rational number is any number that can be expressed as the quotient or fraction p/q, where p and q are integers, and q is not equal to zero. The key here is the ability to represent the number as a fraction of two integers.
Some examples of rational numbers include:
- 1/2: A simple fraction representing one-half.
- 3/4: Three-quarters.
- -5/7: A negative rational number.
- 2: This can be expressed as 2/1, fulfilling the definition.
- 0: Represented as 0/1.
- -6: Represented as -6/1.
Numbers that cannot be expressed as a fraction of two integers are called irrational numbers. Examples include π (pi), √2 (the square root of 2), and e (Euler's number). These numbers have decimal representations that either go on forever without repeating or are non-terminating and non-repeating.
The Quotient of Two Rational Numbers: Proof of Rationality
Now, let's address the core question: if we take any two rational numbers and divide one by the other (find their quotient), will the result always be a rational number? The answer, as previously stated, is yes. We can demonstrate this using a formal proof.
Theorem: The quotient of two rational numbers (where the divisor is not zero) is always a rational number.
Proof:
Let's represent our two rational numbers as:
- a = p/q where p and q are integers, and q ≠ 0
- b = r/s where r and s are integers, and s ≠ 0
Now, let's find the quotient of these two numbers:
a / b = (p/q) / (r/s)
To divide fractions, we multiply the first fraction by the reciprocal of the second fraction:
a / b = (p/q) * (s/r) = (ps) / (qr)
Since p, q, r, and s are all integers, their products (ps) and (qr) are also integers. Let's denote (ps) as m and (qr) as n. Therefore:
a / b = m/n
Where m and n are integers, and provided that b (and therefore r) is not zero, n will also not be zero. This expression perfectly fits the definition of a rational number. Therefore, the quotient of two rational numbers is always a rational number.
Illustrative Examples
Let's solidify our understanding with some concrete examples:
Example 1:
- a = 2/3
- b = 4/5
a / b = (2/3) / (4/5) = (2/3) * (5/4) = 10/12 = 5/6 (simplifying the fraction)
The result, 5/6, is clearly a rational number.
Example 2:
- a = -7/8
- b = 1/2
a / b = (-7/8) / (1/2) = (-7/8) * (2/1) = -14/8 = -7/4
Again, -7/4 is a rational number.
Example 3: Involving Integers
- a = 5 (which is 5/1)
- b = 3 (which is 3/1)
a / b = (5/1) / (3/1) = (5/1) * (1/3) = 5/3
The result is a rational number. This shows that the theorem holds true even when one or both of the rational numbers are integers.
Addressing Potential Objections and Special Cases
One might argue about division by zero. However, the theorem explicitly states that the divisor (b) cannot be zero. Division by zero is undefined in mathematics and is not a counterexample to the theorem. It simply highlights a condition that must be met for the theorem to hold true.
Another point to consider is the simplification of fractions. The result of dividing two rational numbers might initially appear as a fraction that can be simplified further. However, even the unsimplified fraction fits the definition of a rational number because the numerator and denominator remain integers.
Conclusion: The Robustness of Rational Number Properties
This comprehensive analysis demonstrates definitively that the quotient of two rational numbers (provided the divisor is not zero) is always a rational number. This property is a cornerstone of number theory and highlights the inherent structure and consistency within the set of rational numbers. Understanding this fundamental concept is crucial for further exploration of more advanced mathematical topics, such as algebraic structures, field theory, and real analysis. The proof presented, along with the illustrative examples, provides a solid foundation for grasping this important mathematical truth. The consistency of this property emphasizes the elegance and predictability of operations within the system of rational numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about Is The Quotient Of Two Rational Numbers Always Rational . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.