Is The Square Root Of 20 A Rational Number
News Co
May 07, 2025 · 5 min read
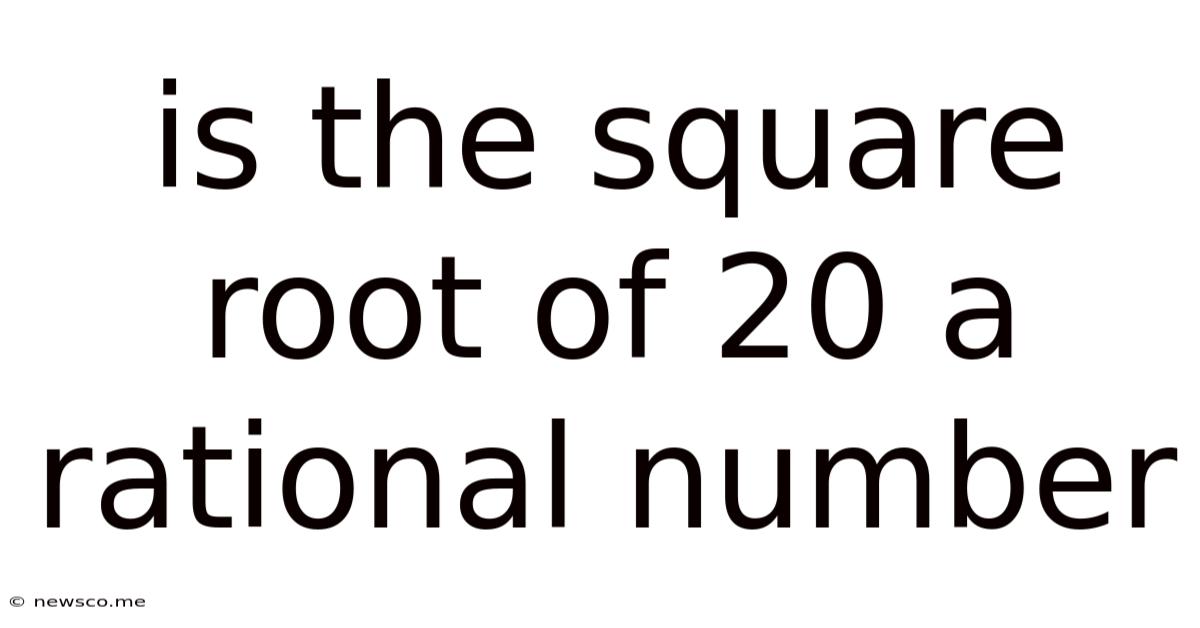
Table of Contents
Is the Square Root of 20 a Rational Number? A Deep Dive into Irrationality
The question of whether the square root of 20 is a rational number is a fundamental concept in mathematics, touching upon the core distinctions between rational and irrational numbers. Understanding this requires a solid grasp of number systems and proof techniques. This article will not only answer the question definitively but also explore the broader implications and related concepts.
Understanding Rational and Irrational Numbers
Before we delve into the specifics of √20, let's establish a clear understanding of rational and irrational numbers.
Rational Numbers: A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p is the numerator and q is the non-zero denominator. Examples include 1/2, 3, -4/7, and 0 (which can be expressed as 0/1). Essentially, rational numbers can be represented precisely as a ratio of two whole numbers.
Irrational Numbers: Irrational numbers, conversely, cannot be expressed as a simple fraction of two integers. Their decimal representations are non-terminating (they don't end) and non-repeating (they don't have a repeating pattern). Famous examples include π (pi) and e (Euler's number). The square root of many numbers is also irrational.
Proving the Irrationality of √20
To determine if √20 is rational or irrational, we'll employ a proof by contradiction. This method assumes the opposite of what we want to prove and then shows that this assumption leads to a logical contradiction.
Step 1: The Assumption
Let's assume, for the sake of contradiction, that √20 is a rational number. This means it can be expressed as a fraction p/q, where p and q are integers, q ≠ 0, and the fraction is in its simplest form (meaning p and q have no common factors other than 1).
Step 2: Manipulating the Equation
If √20 = p/q, then squaring both sides gives us:
20 = p²/q²
Multiplying both sides by q² yields:
20q² = p²
Step 3: Deductions about Divisibility
This equation tells us that p² is an even number (since it's equal to 20q², which is a multiple of 2). If p² is even, then p itself must also be even. This is because the square of an odd number is always odd. Since p is even, we can express it as 2k, where k is another integer.
Substituting p = 2k into the equation 20q² = p², we get:
20q² = (2k)²
20q² = 4k²
Dividing both sides by 4:
5q² = k²
Step 4: The Contradiction
This equation shows that k² is a multiple of 5, implying that k itself is also a multiple of 5 (similar to the reasoning with p and 2). Therefore, we can express k as 5m, where m is another integer.
Substituting k = 5m back into 5q² = k², we get:
5q² = (5m)²
5q² = 25m²
Dividing both sides by 5:
q² = 5m²
This equation reveals that q² is also a multiple of 5, meaning q must be a multiple of 5.
Step 5: The Conclusion
We've now shown that both p and q are multiples of 5. This directly contradicts our initial assumption that p/q is in its simplest form (no common factors other than 1). This contradiction proves that our initial assumption – that √20 is rational – must be false.
Therefore, √20 is an irrational number.
Simplifying √20 and Understanding its Irrationality
While we've proven √20's irrationality, we can simplify it to a certain extent. We can rewrite 20 as 4 * 5. Since √4 = 2, we can simplify √20 as follows:
√20 = √(4 * 5) = √4 * √5 = 2√5
This shows that √20 is a multiple of the irrational number √5. Since the product of a rational number (2) and an irrational number (√5) is always irrational, this further supports our conclusion.
Exploring Related Concepts and Further Applications
Understanding the irrationality of √20 connects to several important mathematical concepts:
1. Pythagorean Theorem and Irrational Numbers: The discovery of irrational numbers is often linked to the Pythagorean theorem (a² + b² = c²). Early mathematicians realized that the diagonal of a square with sides of length 1 (which is √2) couldn't be expressed as a ratio of integers, leading to a crisis in their understanding of numbers. The irrationality of √20 extends this concept.
2. Continued Fractions: Irrational numbers can be represented as continued fractions—an infinite expression of fractions within fractions. The continued fraction representation of √20 provides another way to demonstrate its irrationality.
3. Decimal Expansion: The decimal expansion of √20 is non-terminating and non-repeating, which is another characteristic of irrational numbers. While we can approximate it, we cannot write it down exactly as a decimal.
4. Approximations and Applications: Even though √20 is irrational, we can use rational approximations for practical applications. For example, in engineering or construction, a sufficiently precise decimal approximation might suffice for calculations.
Conclusion: The Significance of Irrational Numbers
The seemingly simple question of whether √20 is rational or irrational leads us to a deeper appreciation of the richness and complexity of the number system. Understanding the distinction between rational and irrational numbers, and the methods for proving irrationality, is crucial for anyone pursuing a deeper understanding of mathematics. The concepts explored here have far-reaching implications across various fields, highlighting the fundamental importance of irrational numbers in both theoretical mathematics and real-world applications. The proof by contradiction, demonstrated in this article, is a powerful tool in mathematical reasoning and highlights the elegance and logic inherent in mathematical proofs.
Latest Posts
Latest Posts
-
Derivative Of 4 Square Root X
May 08, 2025
-
789 091 To The Nearest Ten Thousand
May 08, 2025
-
How To Write 45 Dollars On A Check
May 08, 2025
-
Which Of The Following Is An Improper Fraction
May 08, 2025
-
How To Convert Ln To E
May 08, 2025
Related Post
Thank you for visiting our website which covers about Is The Square Root Of 20 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.