Is The Square Root Of 27 A Rational Number
News Co
Mar 25, 2025 · 5 min read
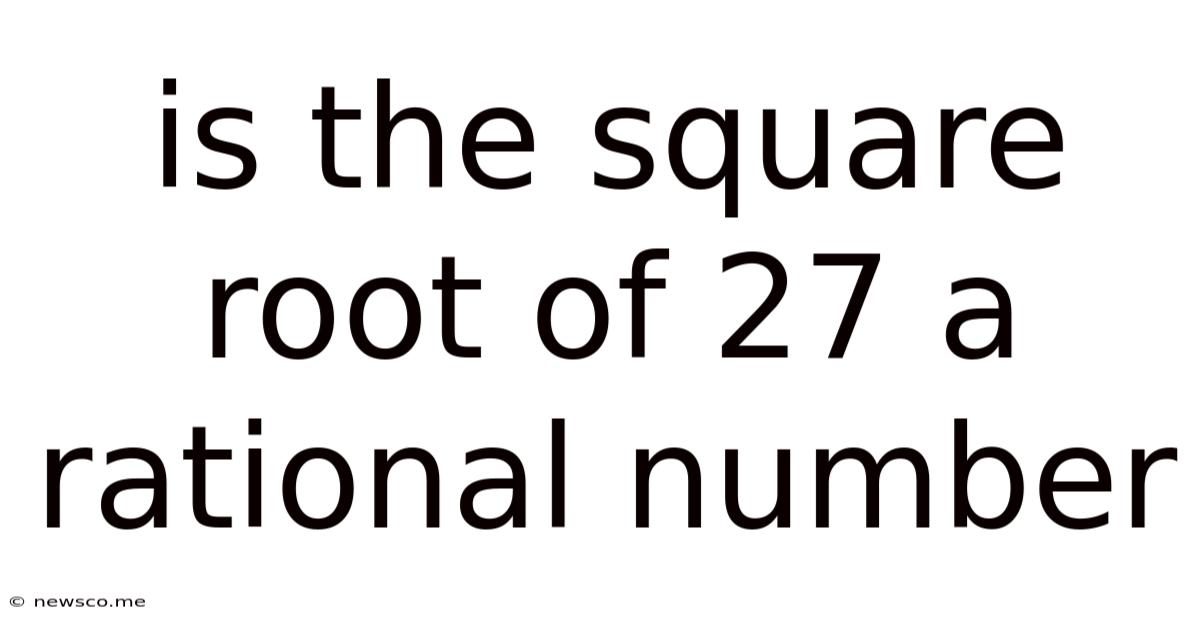
Table of Contents
Is the Square Root of 27 a Rational Number? A Deep Dive into Irrationality
The question of whether the square root of 27 is a rational number is a fundamental one in mathematics, touching upon the core concepts of rational and irrational numbers. Understanding this requires a solid grasp of these definitions and some key mathematical properties. This article will not only answer the question definitively but also explore the broader implications and related concepts.
Understanding Rational and Irrational Numbers
Before diving into the specifics of √27, let's establish a clear understanding of the terms:
Rational Numbers: A rational number is any number that can be expressed as a fraction p/q, where 'p' and 'q' are integers, and 'q' is not equal to zero. Examples include 1/2, 3/4, -5/7, and even integers like 4 (which can be written as 4/1). The decimal representation of a rational number either terminates (e.g., 0.75) or repeats infinitely with a predictable pattern (e.g., 0.333...).
Irrational Numbers: Irrational numbers, on the other hand, cannot be expressed as a fraction of two integers. Their decimal representations are non-terminating and non-repeating. Famous examples include π (pi) and e (Euler's number). The square root of many numbers, particularly non-perfect squares, also falls into this category.
Investigating the Square Root of 27
Now, let's focus on √27. To determine if it's rational or irrational, we can employ several approaches:
1. Simplification and Prime Factorization
The first step is to simplify √27. We can do this by finding its prime factorization:
27 = 3 x 3 x 3 = 3³
Therefore, √27 = √(3³)= √(9 x 3) = √9 x √3 = 3√3
This simplification reveals that √27 is equal to 3 multiplied by the square root of 3. Since 3 is a rational number, the rationality of √27 hinges on the rationality of √3.
2. Proof by Contradiction (for √3, and therefore √27)
A classic method for proving the irrationality of a number is proof by contradiction. Let's assume, for the sake of contradiction, that √3 is a rational number. This means it can be expressed as a fraction p/q, where p and q are integers, q ≠ 0, and the fraction is in its simplest form (meaning p and q share no common factors other than 1).
So, we have:
√3 = p/q
Squaring both sides:
3 = p²/q²
Rearranging:
3q² = p²
This equation tells us that p² is a multiple of 3. Since 3 is a prime number, this implies that p itself must also be a multiple of 3. We can express this as:
p = 3k (where k is an integer)
Substituting this back into the equation 3q² = p²:
3q² = (3k)² = 9k²
Dividing both sides by 3:
q² = 3k²
This shows that q² is also a multiple of 3, and therefore q must be a multiple of 3.
We've now reached a contradiction. We initially assumed that p/q was in its simplest form (no common factors). However, we've shown that both p and q are multiples of 3, meaning they have a common factor of 3. This contradiction proves our initial assumption – that √3 is rational – must be false. Therefore, √3 is irrational.
Since √27 = 3√3, and √3 is irrational, and multiplying an irrational number by a rational number still results in an irrational number, we conclude that √27 is irrational.
Further Exploration of Irrational Numbers and their Properties
The irrationality of √27 is not an isolated case. Many square roots of non-perfect squares are irrational. Understanding the properties of irrational numbers is crucial in various mathematical fields:
-
Geometry: Irrational numbers frequently appear in geometric calculations, particularly when dealing with lengths and areas of figures involving non-right angles. The diagonal of a square with sides of length 1, for example, is √2 – an irrational number.
-
Calculus: Irrational numbers play a vital role in calculus, especially when dealing with limits, derivatives, and integrals. Many important mathematical constants, like e and π, are irrational.
-
Number Theory: The study of irrational numbers significantly contributes to number theory, a branch of mathematics focused on the properties of integers. Understanding the distribution and properties of irrational numbers is a major area of research.
-
Approximations: Because irrational numbers have non-terminating decimal expansions, we often use rational approximations to work with them in practical applications. For instance, we might use 1.732 as an approximation for √3. The accuracy of these approximations depends on the application's requirements.
Practical Implications and Applications
While the concept of irrational numbers might seem abstract, they have tangible applications:
-
Construction and Engineering: Accurate calculations involving irrational numbers are essential in many aspects of construction and engineering. For example, the accurate measurement of distances and angles is often dependent upon working with irrational numbers.
-
Computer Science: Representing and manipulating irrational numbers in computer systems is a challenging task. Special algorithms and data structures are necessary for accurate calculations and simulations involving these numbers.
-
Physics: Many physical phenomena involve irrational numbers. For instance, the relationship between the circumference and diameter of a circle is π, an irrational constant that appears repeatedly in physics calculations.
Conclusion: The Irrationality of √27 and its Significance
We have conclusively demonstrated that the square root of 27 is an irrational number. This understanding stems from the fundamental definitions of rational and irrational numbers and a clear understanding of the properties of prime factorization and proof by contradiction. The broader significance of this result lies in its contribution to our understanding of the real number system, and the frequent appearance of irrational numbers in various fields of mathematics and science. The concept, while seemingly abstract, underlies numerous practical applications and computations. Mastering the distinction between rational and irrational numbers, and the methods for determining the nature of a given number, is a crucial step in advancing mathematical literacy and problem-solving skills. The seemingly simple question, "Is the square root of 27 a rational number?", thus opens up a pathway to a deeper appreciation of the richness and complexity of mathematics.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Is The Square Root Of 27 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.