Lcm Of 10 5 And 3
News Co
May 07, 2025 · 5 min read
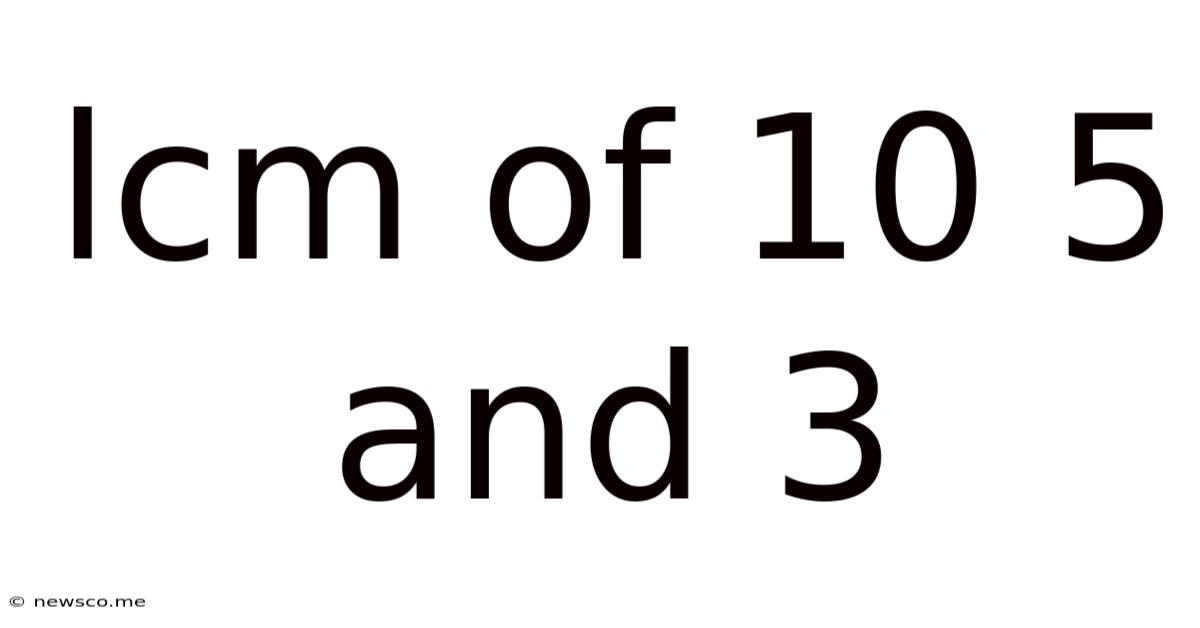
Table of Contents
Finding the Least Common Multiple (LCM) of 10, 5, and 3: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to calculate the LCM is crucial for various applications, from simplifying fractions to solving problems involving cyclical events. This article will delve into the intricacies of finding the LCM of 10, 5, and 3, exploring various methods and providing a comprehensive understanding of the underlying principles.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as its factors. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
This concept extends to more than two numbers. Finding the LCM of multiple numbers is essential in various mathematical contexts, including:
- Fraction Simplification: Determining the least common denominator (LCD) when adding or subtracting fractions. The LCD is the LCM of the denominators.
- Cyclic Events: Solving problems involving events that repeat at different intervals, such as determining when two or more events will occur simultaneously.
- Modular Arithmetic: Used in cryptography and other areas requiring cyclical patterns.
Methods for Calculating LCM
Several methods exist for calculating the least common multiple, each with its own advantages and disadvantages. Let's examine the most common approaches:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. It involves listing the multiples of each number until a common multiple is found. The smallest common multiple is the LCM.
Let's illustrate this with the numbers 10, 5, and 3:
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
By comparing the lists, we can see that 30 is the smallest number present in all three lists. Therefore, the LCM of 10, 5, and 3 is 30.
This method becomes less efficient with larger numbers, as listing multiples can be time-consuming.
2. Prime Factorization Method
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors.
Let's apply this method to 10, 5, and 3:
- Prime factorization of 10: 2 x 5
- Prime factorization of 5: 5
- Prime factorization of 3: 3
The prime factors involved are 2, 3, and 5. We take the highest power of each prime factor:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Now, multiply these highest powers together: 2 x 3 x 5 = 30
Therefore, the LCM of 10, 5, and 3 is 30. This method is significantly more efficient for larger numbers and provides a systematic approach.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship can be extended to more than two numbers, although the calculation becomes more complex.
First, we need to find the GCD of 10, 5, and 3. The GCD is the largest number that divides all three numbers without leaving a remainder. In this case, the GCD of 10, 5, and 3 is 1 (because 1 is the only common divisor).
However, this method is less practical for finding the LCM directly when dealing with more than two numbers. While the relationship holds, calculating the GCD for multiple numbers can be computationally intensive. The prime factorization method is generally preferred for its efficiency in these scenarios.
Applying the LCM to Real-World Problems
Understanding the LCM has practical applications in various scenarios:
1. Scheduling and Timing
Imagine two machines operating on a cycle. Machine A completes a cycle every 10 minutes, Machine B every 5 minutes, and Machine C every 3 minutes. To determine when all three machines will complete a cycle simultaneously, we need to find the LCM of 10, 5, and 3. The LCM is 30, meaning all three machines will complete a cycle simultaneously after 30 minutes.
2. Fraction Arithmetic
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial. This LCM becomes the least common denominator (LCD), allowing us to add or subtract the fractions effectively. For example, if we need to add 1/10 + 1/5 + 1/3, the LCD is 30. The fractions would then become 3/30 + 6/30 + 10/30, resulting in a sum of 19/30.
3. Modular Arithmetic and Cryptography
LCM plays a vital role in modular arithmetic, the foundation of many cryptographic systems. In modular arithmetic, calculations are performed within a fixed range (modulo). Understanding LCM helps in determining the period or cycle length of such calculations.
Conclusion
Finding the least common multiple (LCM) is a crucial skill in mathematics with numerous practical applications. While the listing multiples method is simple for small numbers, the prime factorization method provides a more efficient and systematic approach, especially for larger numbers. Understanding the LCM's relationship with the greatest common divisor (GCD) provides another perspective, but prime factorization is generally more effective for calculating the LCM of multiple numbers directly. The ability to calculate the LCM efficiently is essential for solving problems related to scheduling, fraction arithmetic, and even sophisticated mathematical fields like cryptography. Mastering this concept strengthens your mathematical foundation and opens doors to more complex mathematical explorations.
Latest Posts
Latest Posts
-
Write The Ordered Pairs For The Relation
May 07, 2025
-
Does A Circle Have Line Symmetry
May 07, 2025
-
What Is 2 Divided By 2 3 In Fraction Form
May 07, 2025
-
Equal Sign With Slash Through It
May 07, 2025
-
How Many Inches Equal A Meter
May 07, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 10 5 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.