Lcm Of 12 8 And 10
News Co
Apr 18, 2025 · 5 min read
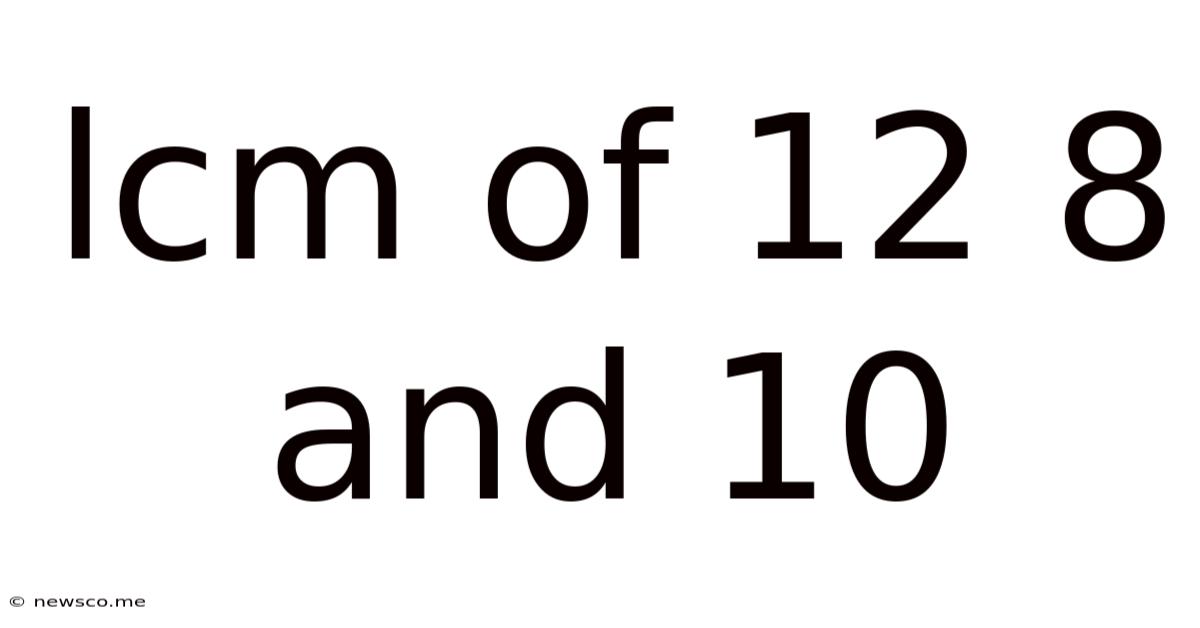
Table of Contents
Finding the LCM of 12, 8, and 10: A Comprehensive Guide
Finding the least common multiple (LCM) of numbers is a fundamental concept in mathematics with applications ranging from simple arithmetic to complex scheduling problems. This article delves deep into calculating the LCM of 12, 8, and 10, exploring various methods and providing a thorough understanding of the underlying principles. We’ll also examine the broader context of LCMs and their practical uses.
Understanding Least Common Multiples (LCM)
Before tackling the specific problem of finding the LCM of 12, 8, and 10, let's establish a solid foundation. The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the given integers without leaving a remainder. For example, the LCM of 2 and 3 is 6, because 6 is the smallest positive integer divisible by both 2 and 3.
Why are LCMs Important?
LCMs are crucial in various mathematical and real-world scenarios:
- Fraction Arithmetic: Finding a common denominator when adding or subtracting fractions requires determining the LCM of the denominators.
- Scheduling Problems: Determining when events with different repeating cycles will occur simultaneously, like buses arriving at a stop or machines completing cycles in a factory.
- Modular Arithmetic: Solving congruences and related problems in number theory.
- Pattern Recognition: Identifying repeating patterns in sequences and series.
Methods for Finding the LCM of 12, 8, and 10
Several methods can be employed to determine the LCM of 12, 8, and 10. Let's explore the most common and efficient approaches:
1. Listing Multiples Method
This is a straightforward but potentially time-consuming method, especially for larger numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120...
By comparing the lists, we observe that the smallest common multiple is 120. Therefore, the LCM(12, 8, 10) = 120.
2. Prime Factorization Method
This method is generally more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 12: 2² x 3
- Prime factorization of 8: 2³
- Prime factorization of 10: 2 x 5
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Now, multiply these highest powers together: 8 x 3 x 5 = 120. Therefore, the LCM(12, 8, 10) = 120.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of a set of numbers are related through the following formula:
LCM(a, b, c) x GCD(a, b, c) = a x b x c
While this method might seem more complex, it provides a powerful alternative, especially when dealing with larger numbers. We can use the Euclidean algorithm to efficiently find the GCD.
First, let's find the GCD of 12, 8, and 10 using the Euclidean algorithm or prime factorization. The GCD(12, 8, 10) = 2.
Now, using the formula:
LCM(12, 8, 10) = (12 x 8 x 10) / GCD(12, 8, 10) = (960) / 2 = 120
Therefore, the LCM(12, 8, 10) = 120.
Comparison of Methods
Each method has its strengths and weaknesses:
- Listing Multiples: Simple to understand but can be inefficient for larger numbers.
- Prime Factorization: Generally more efficient, especially for larger numbers, but requires knowledge of prime factorization.
- GCD Method: Efficient for larger numbers but requires understanding of GCD calculation and the relationship between LCM and GCD.
Practical Applications of LCM
The concept of LCM has numerous practical applications beyond the realm of pure mathematics. Here are a few examples:
-
Recipe Scaling: Imagine you have a recipe that calls for 12 ounces of flour, 8 ounces of sugar, and 10 ounces of butter. To scale the recipe up while maintaining the same proportions, you would find the LCM of 12, 8, and 10 (which is 120). You would then multiply the amount of each ingredient by the factor that gets you to 120. The new recipe would use 120 ounces of flour, 120 ounces of sugar, and 120 ounces of butter. (Though, proportionally, this would result in a huge amount of baked goods)
-
Synchronization of Events: Imagine three machines in a factory complete cycles in 12, 8, and 10 minutes, respectively. To determine when all three machines will simultaneously finish a cycle, you would find the LCM of 12, 8, and 10, which is 120 minutes, or 2 hours.
-
Scheduling Appointments: If you have appointments that repeat every 12 days, 8 days, and 10 days, the LCM will help you determine when all three appointments will coincide.
Conclusion: The LCM of 12, 8, and 10 is 120
We've explored multiple methods for calculating the LCM of 12, 8, and 10, confirming that the answer is indeed 120. Understanding the different methods empowers you to choose the most appropriate approach based on the complexity of the numbers involved. Moreover, the concept of LCM extends far beyond simple arithmetic problems, playing a significant role in various practical applications across different fields. Remember, mastering the LCM concept strengthens your mathematical foundation and opens doors to solving a wider range of problems. Whether you're working on fraction arithmetic, scheduling tasks, or optimizing factory processes, understanding the LCM is a valuable skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 12 8 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.