Lcm Of 2 7 And 3
News Co
Apr 24, 2025 · 5 min read
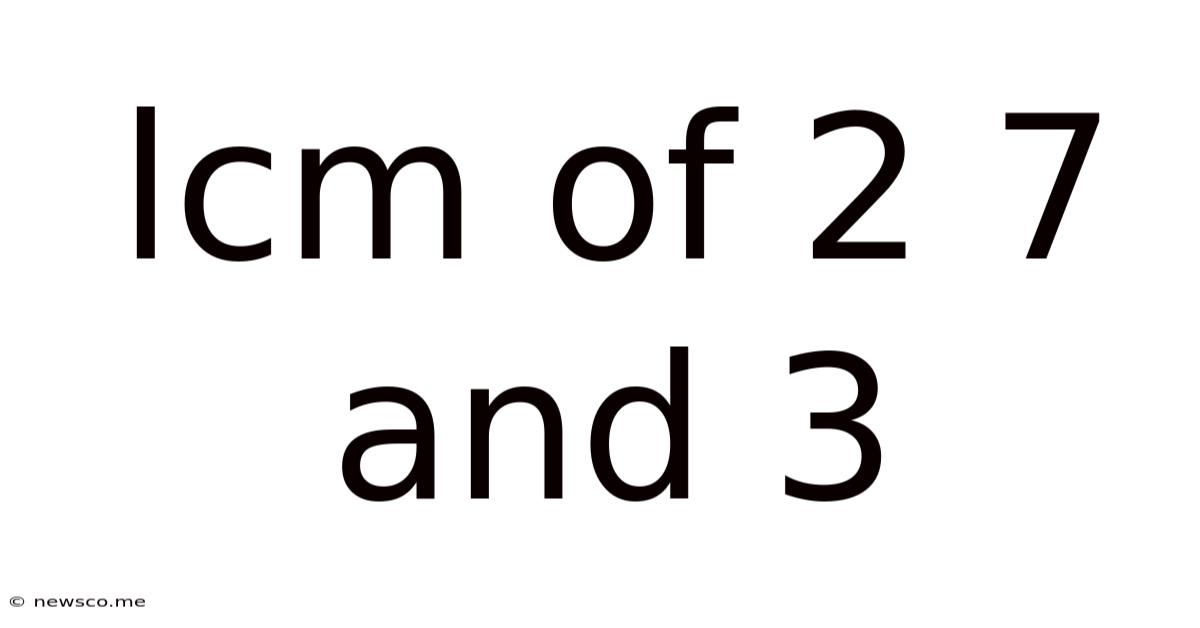
Table of Contents
Understanding the Least Common Multiple (LCM): A Deep Dive with Examples
The Least Common Multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. It plays a crucial role in various applications, from simplifying fractions to solving complex problems in algebra and beyond. This comprehensive guide will explore the LCM, its calculation methods, practical applications, and provide a thorough understanding of how to find the LCM of any set of numbers, including the specific example of finding the LCM of 2, 7, and 3.
What is the Least Common Multiple (LCM)?
The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the numbers in the set as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
Key Characteristics of the LCM:
- Positive Integer: The LCM is always a positive integer.
- Divisibility: The LCM is divisible by each of the integers in the set.
- Smallest: It's the smallest such positive integer that satisfies the divisibility condition.
Methods for Calculating the LCM
Several methods can be employed to determine the LCM of a set of integers. Let's examine the most common ones:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. You list the multiples of each number until you find the smallest multiple common to all.
Example: Finding the LCM of 2 and 3
- Multiples of 2: 2, 4, 6, 8, 10, 12...
- Multiples of 3: 3, 6, 9, 12, 15...
The smallest common multiple is 6. Therefore, LCM(2, 3) = 6.
This method becomes less efficient with larger numbers or a greater number of integers.
2. Prime Factorization Method
This method is more efficient for larger numbers and multiple integers. It involves finding the prime factorization of each number and then constructing the LCM from the highest powers of each prime factor present.
Steps:
- Find the prime factorization of each number: Express each number as a product of its prime factors.
- Identify the highest power of each prime factor: Determine the highest power of each prime factor that appears in any of the factorizations.
- Multiply the highest powers: Multiply these highest powers together to obtain the LCM.
Example: Finding the LCM of 12 and 18
-
Prime factorization:
- 12 = 2² x 3¹
- 18 = 2¹ x 3²
-
Highest powers:
- Highest power of 2: 2² = 4
- Highest power of 3: 3² = 9
-
Multiply: LCM(12, 18) = 2² x 3² = 4 x 9 = 36
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship provides an alternative method for calculating the LCM.
Formula: LCM(a, b) = (a x b) / GCD(a, b)
Example: Finding the LCM of 12 and 18 using the GCD method
- Find the GCD: The GCD of 12 and 18 is 6 (you can find this using the Euclidean algorithm or prime factorization).
- Apply the formula: LCM(12, 18) = (12 x 18) / 6 = 36
This method is particularly efficient when you already know the GCD of the numbers.
Finding the LCM of 2, 7, and 3
Now, let's apply these methods to find the LCM of 2, 7, and 3. The listing multiples method would be cumbersome here, so we'll use the prime factorization method.
-
Prime factorization:
- 2 = 2¹
- 7 = 7¹
- 3 = 3¹
-
Highest powers:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
- Highest power of 7: 7¹ = 7
-
Multiply: LCM(2, 7, 3) = 2 x 3 x 7 = 42
Therefore, the least common multiple of 2, 7, and 3 is 42.
Applications of the LCM
The LCM finds extensive applications in various mathematical and real-world scenarios:
- Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions.
- Solving Problems Involving Cycles or Periodic Events: Determining when events will coincide, such as planetary alignments or cyclical processes.
- Scheduling: Coordinating schedules or events that occur at regular intervals. For instance, determining when two machines operating at different cycles will be synchronized.
- Music Theory: Calculating the least common multiple of note durations helps in understanding musical rhythms and harmony.
- Computer Science: Used in algorithms related to scheduling and synchronization tasks.
Advanced Concepts and Extensions
The concept of LCM extends beyond integers to other mathematical structures. It can be defined for polynomials, rational numbers, and even abstract algebraic structures. These more advanced applications are usually encountered in higher-level mathematics courses.
The understanding of LCM is crucial for any student and professional working with numbers and mathematical operations. Mastering different methods for calculating the LCM ensures the ability to efficiently solve problems across various fields. The use of prime factorization provides a robust and efficient method, especially when dealing with larger numbers or multiple integers. The connection between LCM and GCD provides another valuable tool in the mathematician's toolkit. By understanding both concepts and their relationship, we can solve more advanced and complex mathematical problems. The applications described here highlight the essential role LCM plays not only in abstract mathematics but also in practical real-world scenarios.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 2 7 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.