Lcm Of 2 And 3 And 7
News Co
Apr 19, 2025 · 5 min read
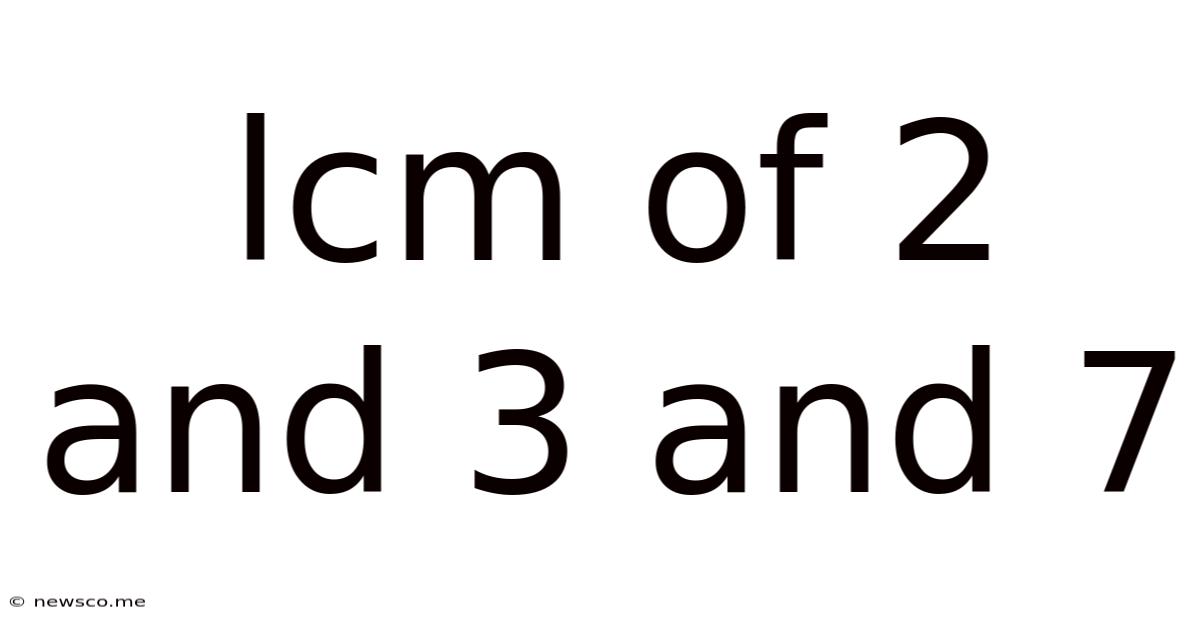
Table of Contents
Finding the Least Common Multiple (LCM) of 2, 3, and 7
The least common multiple (LCM) is a fundamental concept in number theory and arithmetic. It represents the smallest positive integer that is a multiple of all the given integers. Understanding how to calculate the LCM is crucial in various mathematical applications, from simplifying fractions to solving problems in algebra and beyond. This article delves deep into the process of finding the LCM of 2, 3, and 7, explaining various methods and highlighting the significance of this seemingly simple calculation.
Understanding the Concept of LCM
Before we dive into calculating the LCM of 2, 3, and 7, let's solidify our understanding of the core concept. The LCM is the smallest positive integer that is divisible by all the numbers in a given set. For example, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
Notice that the smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
The simplest method, especially for smaller numbers like 2, 3, and 7, is to list the multiples of each number until you find the smallest common multiple. Let's apply this to our set:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42...
- Multiples of 7: 7, 14, 21, 28, 35, 42...
By carefully examining the lists, we can see that the smallest number appearing in all three lists is 42. Therefore, the LCM of 2, 3, and 7 is 42.
Method 2: Prime Factorization
This method is more efficient for larger numbers or a greater number of integers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
Let's break down each number into its prime factors:
- 2: 2 (2 is a prime number)
- 3: 3 (3 is a prime number)
- 7: 7 (7 is a prime number)
Since 2, 3, and 7 are all prime numbers, their prime factorizations are simply themselves. To find the LCM, we multiply the highest power of each prime factor present:
LCM(2, 3, 7) = 2¹ * 3¹ * 7¹ = 42
This method elegantly confirms our result from the listing multiples method. It’s particularly useful when dealing with larger numbers where listing multiples becomes impractical.
Method 3: Using the Formula for Two Numbers and Extending it
While there isn't a direct formula for finding the LCM of three or more numbers at once, we can leverage the formula for two numbers and extend the process iteratively. The formula for the LCM of two numbers, 'a' and 'b', is:
LCM(a, b) = (|a * b|) / GCD(a, b)
Where GCD(a, b) is the greatest common divisor of 'a' and 'b'.
Let's apply this iteratively:
-
Find LCM(2, 3):
- GCD(2, 3) = 1 (2 and 3 share no common factors other than 1)
- LCM(2, 3) = (2 * 3) / 1 = 6
-
Find LCM(6, 7):
- GCD(6, 7) = 1 (6 and 7 share no common factors other than 1)
- LCM(6, 7) = (6 * 7) / 1 = 42
Therefore, the LCM(2, 3, 7) = 42. This method shows how we can break down a multi-number LCM calculation into a series of two-number LCM calculations.
Applications of LCM
The concept of the LCM has numerous applications across various mathematical fields and real-world scenarios:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires determining the LCM of the denominators.
-
Scheduling Problems: Determining when events will coincide, such as the timing of overlapping cycles or the synchronization of repeating tasks. For example, if one machine completes a cycle every 2 hours, another every 3 hours, and a third every 7 hours, the LCM (42 hours) tells you when all three will complete a cycle simultaneously.
-
Modular Arithmetic: The LCM is essential in solving congruence problems and understanding cyclical patterns in number theory.
-
Music Theory: Rhythmic patterns and musical intervals can be analyzed using the concept of LCM.
-
Gears and Sprockets: In mechanical engineering, the LCM is used in determining gear ratios and the synchronization of rotating components.
LCM and GCD: A Complementary Relationship
The least common multiple (LCM) and the greatest common divisor (GCD) are intrinsically linked. For any two integers 'a' and 'b', the following relationship holds true:
LCM(a, b) * GCD(a, b) = a * b
This relationship provides a powerful tool for calculating either the LCM or GCD if the other is known. This property extends beyond just two numbers, although the direct application becomes more complex with more than two integers.
Conclusion: The Significance of LCM(2, 3, 7) = 42
Determining the LCM of 2, 3, and 7, seemingly a simple arithmetic task, highlights the fundamental importance of understanding LCM calculations. Whether you employ the method of listing multiples, prime factorization, or the iterative approach using the two-number LCM formula, the result remains consistent: the LCM(2, 3, 7) = 42. This seemingly simple calculation serves as a cornerstone for more complex mathematical concepts and has practical applications across numerous disciplines. Mastering the various methods for finding the LCM equips you with valuable problem-solving skills applicable far beyond the realm of basic arithmetic. The understanding of LCM lays the foundation for more advanced mathematical explorations and practical problem-solving in diverse fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 2 And 3 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.