Lcm Of 3 10 And 5
News Co
Apr 17, 2025 · 5 min read
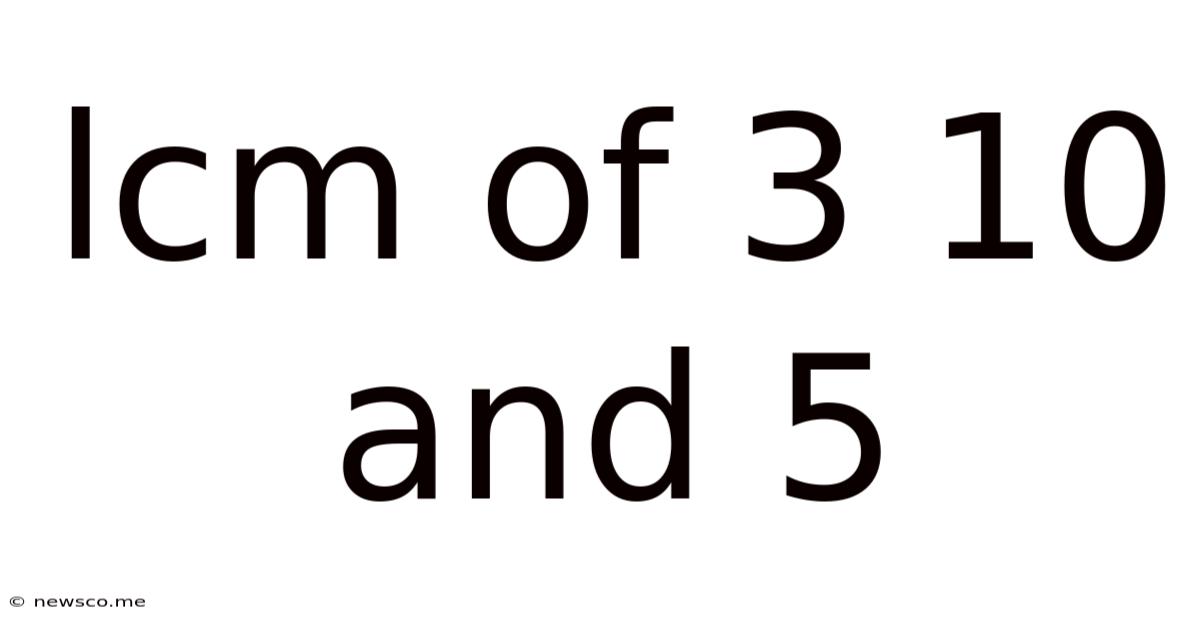
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 10, and 5: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding LCM is crucial for solving various problems involving fractions, ratios, and cyclical events. This comprehensive guide will delve deep into finding the LCM of 3, 10, and 5, explaining multiple methods and exploring the broader implications of this concept.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Methods for Finding the LCM of 3, 10, and 5
There are several ways to calculate the LCM of 3, 10, and 5. Let's explore the most common methods:
1. Listing Multiples Method
This is a straightforward method, especially useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 10: 10, 20, 30, 40, 50...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
By comparing the lists, we can see that the smallest number present in all three lists is 30. Therefore, the LCM of 3, 10, and 5 is 30.
2. Prime Factorization Method
This method is more efficient for larger numbers or when dealing with more than three numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 3: 3
- Prime factorization of 10: 2 x 5
- Prime factorization of 5: 5
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2¹ = 2.
- The highest power of 3 is 3¹ = 3.
- The highest power of 5 is 5¹ = 5.
Multiplying these together: 2 x 3 x 5 = 30. Therefore, the LCM of 3, 10, and 5 is 30.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. While this method is less intuitive for finding the LCM directly, it can be useful in certain contexts. However, for three or more numbers, a direct application of this method becomes complex and less efficient than prime factorization.
Let's illustrate the principle with two numbers first:
Consider finding the LCM of 3 and 10.
- The GCD of 3 and 10 is 1.
- The product of 3 and 10 is 30.
- Therefore, the LCM of 3 and 10 is 30 / 1 = 30.
Extending this to three numbers requires finding the GCD of pairs of numbers and then using a more complex iterative process, making the prime factorization method more practical for our case.
Applications of LCM
The concept of LCM has wide-ranging applications in various fields:
1. Fraction Arithmetic
Finding the LCM is essential when adding or subtracting fractions with different denominators. The LCM of the denominators is used to find the least common denominator (LCD), allowing us to add or subtract the fractions easily.
For example: 1/3 + 1/5 + 1/10. The LCM of 3, 5, and 10 is 30. Converting each fraction to have a denominator of 30 allows for direct addition.
2. Cyclical Events
LCM is used to determine when cyclical events will coincide. For example, if event A occurs every 3 days and event B occurs every 10 days, the LCM will tell us when both events will happen on the same day. In this case, the LCM (3, 10) = 30, meaning both events will coincide every 30 days. Adding a third event occurring every 5 days, using the LCM (3, 10, 5) = 30 indicates the three events will coincide every 30 days.
3. Measurement Conversions
In situations involving conversions between different units of measurement, the LCM can be helpful. For instance, if you need to convert measurements in feet and inches to a common unit, finding the LCM of the denominators simplifies the process.
4. Scheduling and Planning
LCM finds applications in scheduling tasks or events that occur at different intervals. For example, in project management, determining when different phases of a project will align can involve finding the LCM of their respective durations.
5. Number Theory and Abstract Algebra
The LCM plays a significant role in advanced mathematical concepts within number theory and abstract algebra. It relates to modular arithmetic, divisibility rules, and other intricate mathematical structures.
LCM and GCD Relationship: A Deeper Dive
The relationship between the LCM and GCD of two integers a and b is fundamentally important:
LCM(a, b) * GCD(a, b) = a * b
This formula holds true for any two integers. This relationship highlights the inherent connection between these two crucial concepts in number theory. However, generalizing this formula directly to three or more numbers is not straightforward and requires a more complex approach.
Using Technology to Find LCM
While manual calculation is valuable for understanding the underlying concepts, technology offers efficient tools for computing LCMs, especially for larger numbers or numerous inputs. Many calculators and mathematical software packages have built-in functions to calculate the LCM of a set of numbers. Programming languages also provide functions or libraries for such computations. This is particularly helpful when dealing with complex scenarios or when speed and accuracy are paramount.
Conclusion
Understanding the least common multiple is crucial for various mathematical operations and real-world applications. The methods outlined in this guide—listing multiples, prime factorization, and leveraging the GCD—provide a comprehensive approach to calculating the LCM. While the prime factorization method is generally the most efficient and versatile, selecting the appropriate method depends on the context and the complexity of the numbers involved. Remember that the ability to calculate LCM efficiently is a valuable skill in many fields, ranging from basic arithmetic to advanced mathematical disciplines. Mastering these techniques will significantly enhance your problem-solving skills and broaden your understanding of mathematical concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 3 10 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.