Lcm Of 3 4 And 5
News Co
Mar 25, 2025 · 5 min read
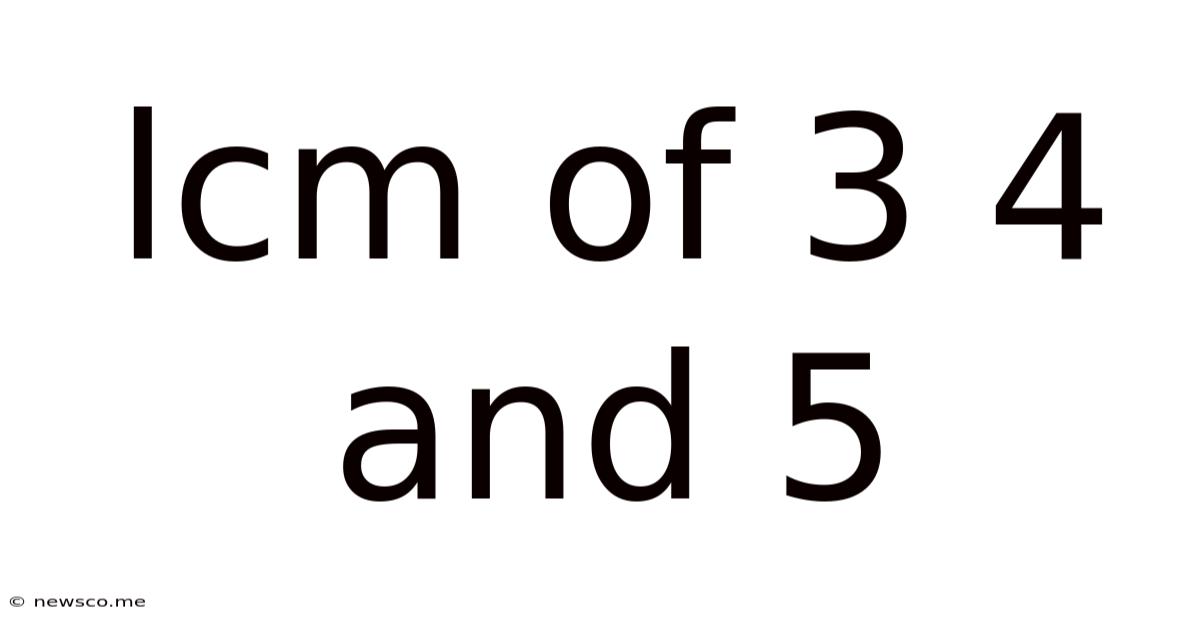
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 4, and 5: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications, from scheduling problems to simplifying fractions. This comprehensive guide delves into the process of finding the LCM of 3, 4, and 5, illustrating various methods and exploring the underlying mathematical principles. We'll also explore real-world applications and provide practice problems to solidify your understanding.
Understanding Least Common Multiples
Before we tackle the LCM of 3, 4, and 5, let's establish a clear understanding of the concept. The LCM of a set of numbers is the smallest positive integer that is divisible by all the numbers in the set. It's the smallest number that contains all the numbers as factors. For instance, the LCM of 2 and 3 is 6, because 6 is the smallest number divisible by both 2 and 3.
Think of it like this: Imagine you have three different gears, one with 3 teeth, one with 4 teeth, and one with 5 teeth. The LCM represents the smallest number of rotations needed for all three gears to simultaneously return to their starting positions.
Methods for Finding the LCM
Several methods exist for determining the LCM of a set of numbers. We'll explore three common approaches: listing multiples, prime factorization, and using the greatest common divisor (GCD).
1. Listing Multiples
This method is straightforward but can be time-consuming for larger numbers. We simply list the multiples of each number until we find the smallest multiple common to all.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60...
By comparing the lists, we observe that the smallest multiple common to 3, 4, and 5 is 60. Therefore, the LCM(3, 4, 5) = 60.
2. Prime Factorization
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM by taking the highest power of each prime factor present in the factorizations.
- Prime factorization of 3: 3 = 3¹
- Prime factorization of 4: 4 = 2²
- Prime factorization of 5: 5 = 5¹
To find the LCM, we take the highest power of each prime factor: 2², 3¹, and 5¹. Multiplying these together, we get:
LCM(3, 4, 5) = 2² * 3 * 5 = 4 * 3 * 5 = 60
3. Using the Greatest Common Divisor (GCD)
The LCM and GCD are closely related. There's a useful formula that connects them:
LCM(a, b) * GCD(a, b) = a * b
This formula can be extended to more than two numbers. However, finding the GCD for multiple numbers requires slightly more complex algorithms like the Euclidean algorithm or its adaptations for multiple numbers. While this method is powerful, for smaller numbers like 3, 4, and 5, the prime factorization method is often simpler.
Let's illustrate the concept:
First, find the GCD of 3, 4, and 5. Since 3, 4, and 5 are all relatively prime (they share no common factors other than 1), the GCD(3, 4, 5) = 1.
While the formula is theoretically applicable for multiple numbers, its direct application becomes more complex. For the numbers 3, 4 and 5, the prime factorization method offers a more straightforward solution.
Real-World Applications of LCM
The LCM has numerous practical applications:
- Scheduling: Imagine three buses arrive at a station at intervals of 3, 4, and 5 hours. The LCM (60 hours) determines when all three buses will arrive at the station simultaneously.
- Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions. It allows us to find a common denominator, making the addition or subtraction easier.
- Project Management: If different tasks in a project take 3, 4, and 5 days respectively, the LCM can help determine the minimum time needed to complete all tasks.
- Music: The LCM is used in music theory to find the least common multiple of the frequencies of different notes to determine the lowest note that will be a harmonic combination of the given notes.
- Cyclic Events: Imagine three events occurring in cycles of 3, 4, and 5 days. The LCM will tell you when all three events will coincide.
These are just a few examples; the applications of LCM are vast and touch upon numerous fields.
Practice Problems
Let's solidify your understanding with a few practice problems:
- Find the LCM of 6, 8, and 10. (Hint: Use prime factorization)
- What is the LCM of 9, 12, and 15? (Hint: You can use any of the methods discussed)
- Three lights flash at intervals of 12 seconds, 15 seconds, and 18 seconds. When will they flash together? (Hint: This is a real-world application of LCM)
- Find the smallest number that is divisible by 2, 3, 5, and 7. (Hint: Prime factorization will be useful here)
Solutions to Practice Problems
-
LCM of 6, 8, and 10:
- 6 = 2 * 3
- 8 = 2³
- 10 = 2 * 5
- LCM(6, 8, 10) = 2³ * 3 * 5 = 120
-
LCM of 9, 12, and 15:
- 9 = 3²
- 12 = 2² * 3
- 15 = 3 * 5
- LCM(9, 12, 15) = 2² * 3² * 5 = 180
-
Three lights flashing: The LCM of 12, 15, and 18 is 180 seconds. Therefore, they will flash together every 180 seconds (or 3 minutes).
-
Smallest number divisible by 2, 3, 5, and 7:
- LCM(2, 3, 5, 7) = 2 * 3 * 5 * 7 = 210
Conclusion
Finding the LCM is a fundamental skill with far-reaching applications. Whether you're solving mathematical problems, scheduling events, or working on projects, understanding LCM provides valuable tools for problem-solving. By mastering the different methods presented in this guide – listing multiples, prime factorization, and using the GCD – you'll be well-equipped to tackle any LCM challenge. Remember to practice regularly to reinforce your understanding and improve your proficiency. The more you practice, the more intuitive this important mathematical concept will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 3 4 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.