Lcm Of 3 5 And 11
News Co
Apr 02, 2025 · 5 min read
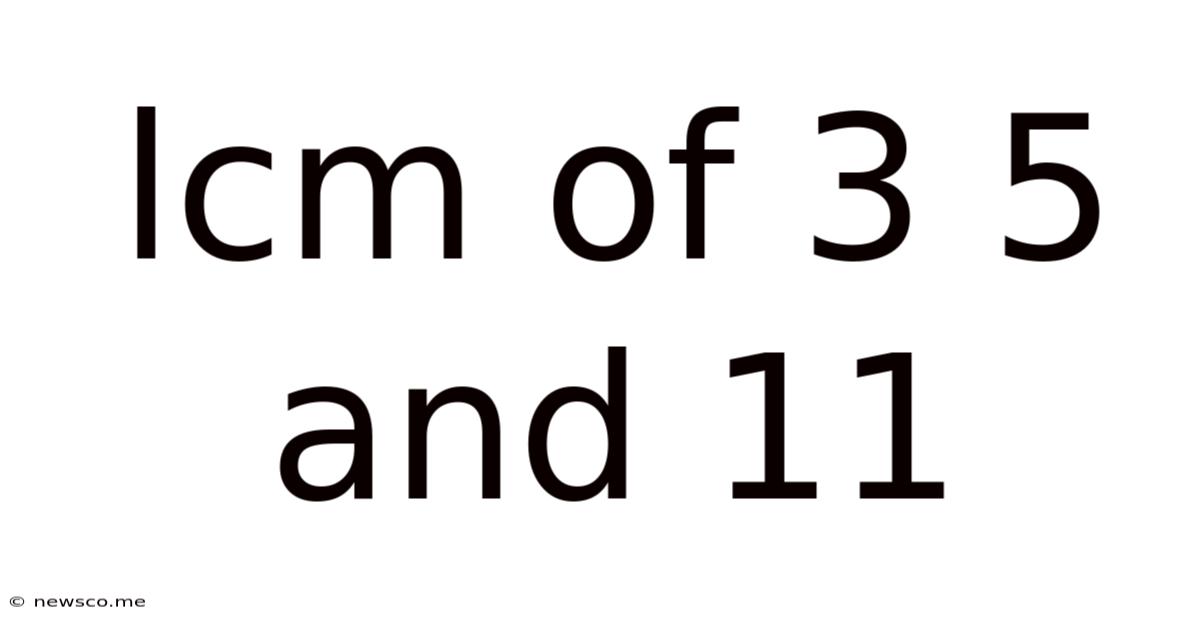
Table of Contents
Finding the LCM of 3, 5, and 11: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in arithmetic and number theory. Understanding how to calculate the LCM is essential for solving various problems, from simplifying fractions to scheduling events. This comprehensive guide dives deep into finding the LCM of 3, 5, and 11, explaining the process in detail and providing multiple methods to achieve the solution. We will also explore the broader applications of LCM and its importance in various mathematical contexts.
Understanding Least Common Multiple (LCM)
Before we delve into calculating the LCM of 3, 5, and 11, let's solidify our understanding of what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as factors.
Example: The LCM of 2 and 3 is 6, because 6 is the smallest positive integer that is divisible by both 2 and 3.
Key Differences between LCM and GCD: It's crucial to distinguish the LCM from the greatest common divisor (GCD). While the LCM is the smallest common multiple, the GCD is the largest common divisor. For instance, the GCD of 12 and 18 is 6, as 6 is the largest number that divides both 12 and 18 without a remainder.
Methods for Finding the LCM of 3, 5, and 11
Several methods can be employed to determine the LCM of 3, 5, and 11. Let's explore the most common and effective approaches.
Method 1: Prime Factorization
This method is considered one of the most efficient ways to calculate the LCM, especially when dealing with larger numbers. It involves breaking down each number into its prime factors.
-
Find the prime factorization of each number:
- 3 = 3 (3 is a prime number)
- 5 = 5 (5 is a prime number)
- 11 = 11 (11 is a prime number)
-
Identify the highest power of each prime factor: In this case, each number is already a prime number, so the highest power of each is simply itself: 3¹, 5¹, and 11¹.
-
Multiply the highest powers together: The LCM is the product of these highest powers.
LCM(3, 5, 11) = 3¹ × 5¹ × 11¹ = 3 × 5 × 11 = 165
Therefore, the least common multiple of 3, 5, and 11 is 165.
Method 2: Listing Multiples
This method is more suitable for smaller numbers. It involves listing the multiples of each number until you find the smallest common multiple.
-
List the multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105, 108, 111, 114, 117, 120, 123, 126, 129, 132, 135, 138, 141, 144, 147, 150, 153, 156, 159, 162, 165,...
-
List the multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 135, 140, 145, 150, 155, 165,...
-
List the multiples of 11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, 143, 154, 165,...
The smallest multiple common to all three lists is 165.
Method 3: Using the Formula (for two numbers only)
This method uses the formula: LCM(a, b) = (|a × b|) / GCD(a, b). While this formula is directly applicable only for two numbers, we can extend it by finding the LCM of two numbers first and then finding the LCM of the result and the third number.
This is less efficient for three or more numbers and the prime factorization method is generally preferred.
Applications of LCM
The LCM has numerous applications across various fields. Here are some examples:
- Fractions: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Scheduling: Determining when events with different repeating cycles will occur simultaneously. For example, if one event occurs every 3 days and another every 5 days, the LCM helps determine when both events will coincide.
- Music: Understanding musical harmony and rhythm involves finding common multiples of note durations.
- Gears: In mechanical engineering, the LCM is used to calculate gear ratios and synchronize the rotation of multiple gears.
- Modular Arithmetic: The LCM plays a significant role in solving congruence problems in modular arithmetic.
- Computer Science: Used in algorithms related to scheduling, synchronization, and optimization problems.
Expanding on the Concept: LCM of More Numbers
The methods described above, particularly prime factorization, can be easily extended to find the LCM of more than three numbers. For instance, to find the LCM of 3, 5, 11, and 7:
-
Prime Factorization:
- 3 = 3
- 5 = 5
- 11 = 11
- 7 = 7
-
Highest Powers: The highest power of each prime factor is 3¹, 5¹, 7¹, and 11¹.
-
Multiplication: LCM(3, 5, 11, 7) = 3 × 5 × 7 × 11 = 1155
Conclusion: Mastering LCM Calculations
Understanding and mastering the calculation of the least common multiple is a valuable skill in mathematics. The prime factorization method provides a robust and efficient approach, particularly when dealing with larger numbers or multiple numbers. While the listing multiples method is suitable for smaller numbers, its practicality diminishes as the numbers increase in size. The formula-based method is limited to only two numbers. By grasping the concept of LCM and employing the appropriate methods, you can confidently solve various mathematical problems and appreciate its diverse applications across numerous fields. Remember to practice these methods regularly to build your proficiency and expand your mathematical understanding. Remember, consistent practice is key to mastering any mathematical concept.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 3 5 And 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.