Lcm Of 3 5 And 9
News Co
Mar 26, 2025 · 5 min read
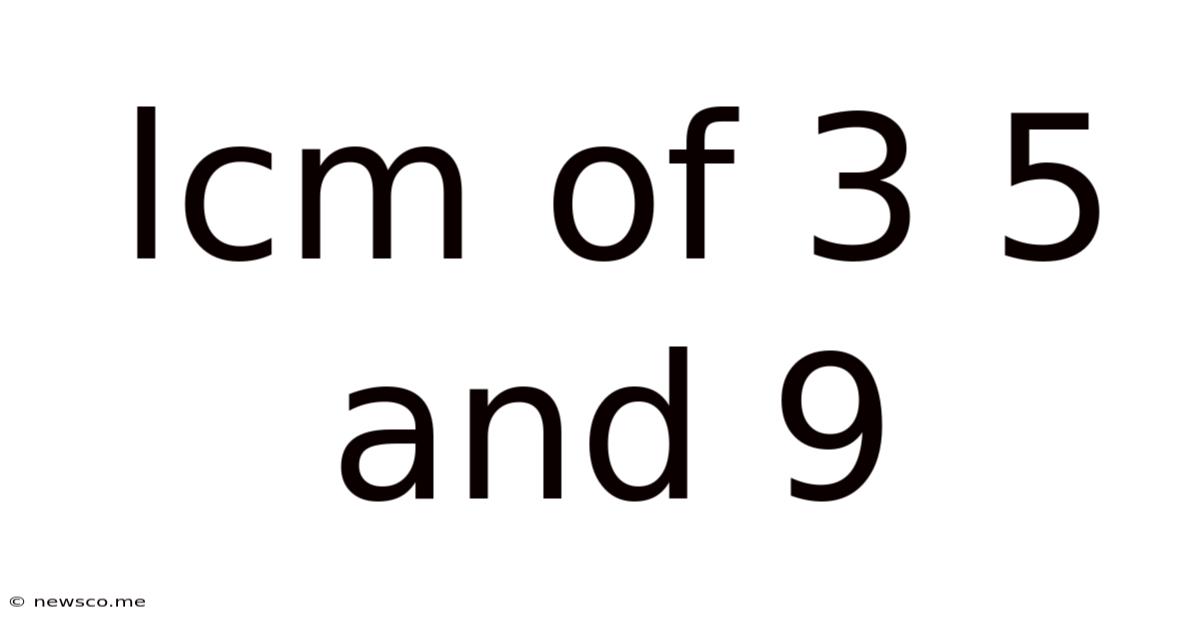
Table of Contents
Finding the LCM of 3, 5, and 9: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications across various fields, from scheduling tasks to simplifying fractions. This comprehensive guide will delve into the process of calculating the LCM of 3, 5, and 9, exploring different methods and providing a solid understanding of the underlying principles. We'll also touch upon the broader applications of LCM calculations.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 3, 5, and 9, let's define the term. The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as factors.
For instance, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
The common multiples of 2 and 3 are 6, 12, 18, 24, and so on. The least common multiple, therefore, is 6.
Methods for Calculating LCM
Several methods exist for calculating the LCM of a set of numbers. We'll explore the three most common approaches:
1. Listing Multiples Method
This is the most straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
Let's apply this to our numbers 3, 5, and 9:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 36, 45, ...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, ...
- Multiples of 9: 9, 18, 27, 36, 45, 54, ...
By examining the lists, we can see that the smallest number common to all three lists is 45. Therefore, the LCM(3, 5, 9) = 45.
This method is simple for small numbers, but it becomes cumbersome and inefficient for larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
Let's break down the prime factorization of 3, 5, and 9:
- 3: 3¹ (3 is a prime number)
- 5: 5¹ (5 is a prime number)
- 9: 3² (9 = 3 x 3)
To find the LCM, we take the highest power of each prime factor present:
- Highest power of 3: 3² = 9
- Highest power of 5: 5¹ = 5
Now, multiply these highest powers together: 9 x 5 = 45
Therefore, the LCM(3, 5, 9) = 45. This method is generally preferred for its efficiency and scalability to larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of a set of numbers are related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship can be extended to more than two numbers, although the calculation becomes slightly more complex.
First, we need to find the GCD of 3, 5, and 9. Since 3, 5, and 9 share no common factors other than 1, their GCD is 1.
Let's use the formula for three numbers a, b, and c:
LCM(a, b, c) = (a x b x c) / GCD(a, b, c)
In our case:
LCM(3, 5, 9) = (3 x 5 x 9) / GCD(3, 5, 9) = 135 / 1 = 45
Therefore, the LCM(3, 5, 9) = 45. This method, while elegant, requires a separate calculation for the GCD, which adds a step to the process.
Applications of LCM Calculations
The calculation of the least common multiple has a wide range of applications across diverse fields:
1. Scheduling and Time Management
Imagine you have three tasks: one that repeats every 3 days, another every 5 days, and a third every 9 days. When will all three tasks coincide again? The answer is the LCM of 3, 5, and 9, which is 45 days. This principle is widely used in scheduling recurring events, appointments, or production cycles.
2. Fraction Simplification
When adding or subtracting fractions, finding the LCM of the denominators is crucial to obtain a common denominator. This simplifies the process and allows for accurate calculations.
3. Number Theory and Cryptography
LCM calculations are fundamental to various concepts in number theory, including modular arithmetic, which plays a crucial role in cryptography and secure communication systems.
4. Music Theory
In music, LCM is used to determine the least common denominator for rhythmic patterns, ensuring a harmonious and synchronized composition.
Choosing the Right Method
The best method for calculating the LCM depends on the numbers involved and your comfort level with different mathematical techniques.
- Listing multiples: Suitable for small numbers where the LCM is easily identifiable.
- Prime factorization: Generally the most efficient and reliable method for larger numbers.
- GCD method: Useful if the GCD is already known or easily calculable.
Conclusion: Mastering LCM Calculations
Understanding how to calculate the least common multiple is a valuable skill with applications extending far beyond simple arithmetic problems. This guide has explored three different methods, highlighting their strengths and weaknesses, allowing you to choose the most appropriate approach for your specific needs. By mastering LCM calculations, you'll be better equipped to tackle a wide range of mathematical and real-world problems. Remember, practice is key to solidifying your understanding and improving your efficiency. Try calculating the LCM of other number sets to reinforce your learning.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 3 5 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.