Lcm Of 3 6 And 9
News Co
Apr 22, 2025 · 5 min read
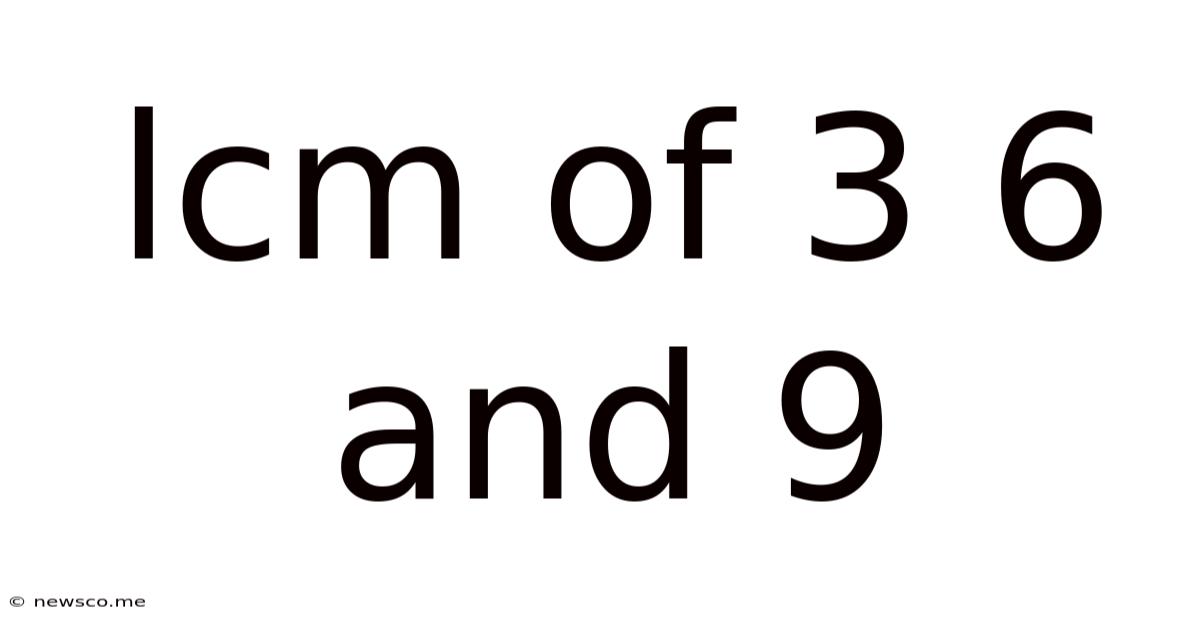
Table of Contents
Finding the LCM of 3, 6, and 9: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with wide-ranging applications in various fields, from scheduling tasks to simplifying fractions and solving complex equations. This comprehensive guide will delve into the process of determining the LCM of 3, 6, and 9, exploring multiple methods and providing a solid understanding of the underlying principles. We'll also examine the practical implications and broader applications of LCM calculations.
Understanding Least Common Multiples (LCM)
Before jumping into the calculation, let's establish a firm grasp of what the least common multiple actually represents. The LCM of two or more integers is the smallest positive integer that is divisible by all the given integers without leaving a remainder. It's the smallest number that contains all the numbers in the set as factors. Think of it as the smallest common "multiple" shared by all the numbers.
Method 1: Listing Multiples
This is a straightforward method, particularly effective for smaller numbers. We simply list the multiples of each number until we find the smallest multiple common to all three.
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
Multiples of 6: 6, 12, 18, 24, 30, 36...
Multiples of 9: 9, 18, 27, 36, 45...
By comparing the lists, we observe that the smallest multiple present in all three lists is 18. Therefore, the LCM of 3, 6, and 9 is 18.
This method is intuitive and easy to understand, making it suitable for beginners. However, it can become cumbersome and time-consuming when dealing with larger numbers or a greater number of integers.
Method 2: Prime Factorization
The prime factorization method is a more efficient and robust technique applicable to any set of numbers, regardless of size. It leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers.
Let's find the prime factorization of each number:
- 3: 3 (3 is a prime number)
- 6: 2 x 3
- 9: 3 x 3 = 3²
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2¹ (from the factorization of 6).
- The highest power of 3 is 3² (from the factorization of 9).
Now, multiply these highest powers together: 2¹ x 3² = 2 x 9 = 18.
Thus, the LCM of 3, 6, and 9, determined using prime factorization, is again 18. This method offers a systematic and efficient approach, particularly beneficial when dealing with larger numbers.
Method 3: Greatest Common Divisor (GCD) and LCM Relationship
The greatest common divisor (GCD) and the least common multiple (LCM) are closely related. For any two integers a and b, the product of their GCD and LCM is equal to the product of the two numbers:
GCD(a, b) x LCM(a, b) = a x b
While this relationship is most directly applied to pairs of numbers, we can extend it to a set of numbers by finding the LCM iteratively. First, we find the LCM of 3 and 6, then use that result to find the LCM with 9.
- GCD(3, 6) = 3
- LCM(3, 6) = (3 x 6) / GCD(3, 6) = 18 / 3 = 6
- GCD(6, 9) = 3
- LCM(6, 9) = (6 x 9) / GCD(6, 9) = 54 / 3 = 18
Therefore, using this iterative GCD approach, we confirm that the LCM of 3, 6, and 9 is 18.
Applications of LCM
The concept of LCM finds applications in various fields:
-
Scheduling: Determining when events will occur simultaneously. For example, if one event occurs every 3 days, another every 6 days, and a third every 9 days, they will all occur together again in 18 days (the LCM of 3, 6, and 9).
-
Fractions: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is the LCM of the denominators.
-
Modular Arithmetic: Used extensively in cryptography and computer science.
-
Music Theory: Determining the harmonic relationships between notes and chords.
-
Engineering: Determining the synchronization of mechanical systems or processes.
LCM and Real-World Scenarios
Let's consider a practical example: Imagine three machines in a factory. Machine A completes a cycle every 3 minutes, Machine B every 6 minutes, and Machine C every 9 minutes. If they all start at the same time, how many minutes will pass before they all complete a cycle simultaneously?
The answer is the LCM of 3, 6, and 9, which, as we've established, is 18 minutes. After 18 minutes, all three machines will have completed a whole number of cycles.
Beyond the Basics: LCM of Larger Numbers
While we've focused on the LCM of 3, 6, and 9, the methods discussed, especially prime factorization, are readily adaptable to larger and more complex sets of numbers. The key is to systematically apply the principles and choose the most efficient method based on the numbers involved. For significantly larger numbers, computational tools or algorithms may be necessary for quick and accurate calculation.
Conclusion: Mastering LCM Calculations
Understanding and calculating the least common multiple is a crucial skill with practical applications across many areas. This guide has explored various methods, highlighting their strengths and weaknesses, ultimately demonstrating that the LCM of 3, 6, and 9 is 18. By mastering these techniques, you'll be equipped to tackle LCM problems with confidence and apply this fundamental mathematical concept to a wide range of real-world scenarios. Remember to choose the method best suited to the numbers involved, prioritizing efficiency and accuracy. The prime factorization method, in particular, provides a reliable and powerful approach applicable to virtually any set of integers.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 3 6 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.