Lcm Of 3 9 And 15
News Co
Mar 28, 2025 · 5 min read
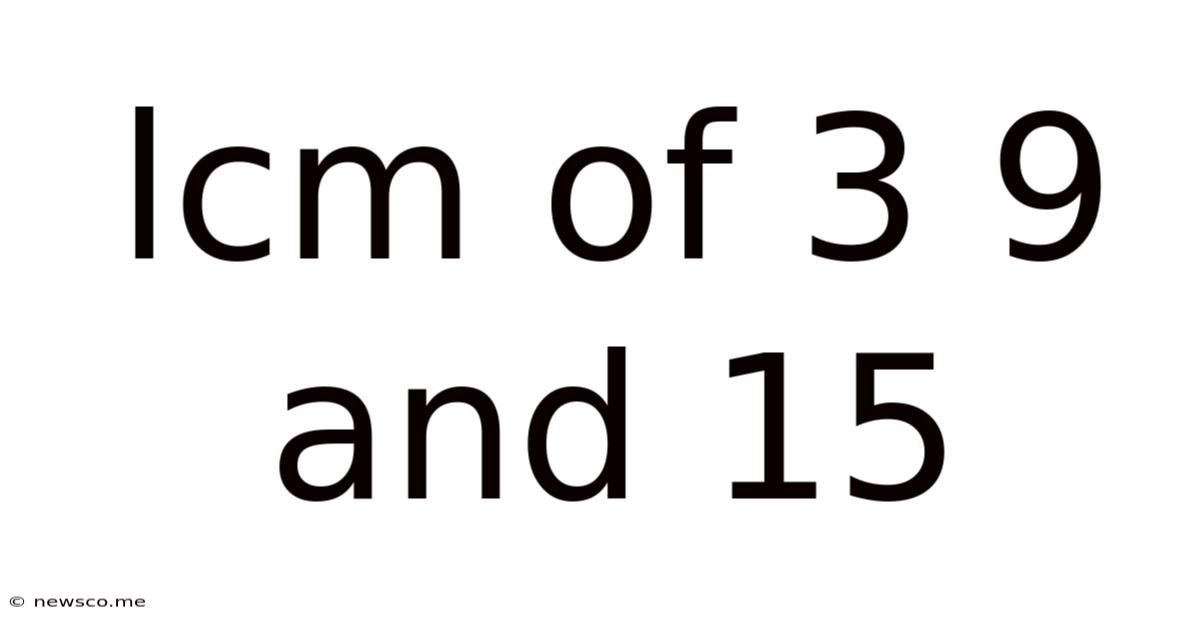
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 9, and 15: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly useful in various fields like fractions, scheduling, and even music theory. This comprehensive guide will delve into the process of determining the LCM of 3, 9, and 15, exploring multiple methods and providing a deeper understanding of the underlying principles. We'll also explore the broader implications of LCM and its applications.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 3, 9, and 15, let's establish a solid understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12… Multiples of 3 are 3, 6, 9, 12, 15… The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 9: 9, 18, 27, 36, 45, 54...
- Multiples of 15: 15, 30, 45, 60...
By comparing these lists, we can see that the smallest number appearing in all three lists is 45. Therefore, the LCM of 3, 9, and 15 is 45.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It involves finding the prime factorization of each number and then constructing the LCM from those prime factors.
-
Find the prime factorization of each number:
- 3 = 3
- 9 = 3 x 3 = 3²
- 15 = 3 x 5
-
Identify the highest power of each prime factor:
- The prime factors are 3 and 5.
- The highest power of 3 is 3² = 9.
- The highest power of 5 is 5¹ = 5.
-
Multiply the highest powers together:
- LCM(3, 9, 15) = 3² x 5 = 9 x 5 = 45
Method 3: Greatest Common Divisor (GCD) Method
This method uses the relationship between the LCM and the greatest common divisor (GCD) of two or more numbers. The formula connecting LCM and GCD is:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers. However, it's generally more complex for multiple numbers and requires iterative calculations of GCDs. Let's illustrate with our example:
-
Find the GCD of 3 and 9: The GCD(3,9) = 3.
-
Find the GCD of 3 and 15: The GCD(3, 15) = 3.
-
Find the GCD of 9 and 15: The GCD(9, 15) = 3.
Although this method establishes the GCD, directly calculating the LCM using the above formula for three or more numbers becomes quite involved. The prime factorization method remains significantly more efficient in this instance.
Applications of LCM
The concept of LCM has wide-ranging applications in various fields:
-
Fraction Arithmetic: Finding the least common denominator (LCD) when adding or subtracting fractions is essentially finding the LCM of the denominators. For example, to add 1/3 + 1/9 + 1/15, we need the LCM of 3, 9, and 15, which is 45.
-
Scheduling: LCM is crucial in solving scheduling problems. For instance, if three buses depart from a station at intervals of 3, 9, and 15 minutes, respectively, the LCM (45 minutes) determines when all three buses will depart simultaneously again.
-
Music Theory: LCM is used to calculate the least common period of musical notes with different durations.
-
Engineering and Construction: In projects involving repetitive cycles or patterns, LCM helps in determining the optimal synchronization points.
-
Computer Science: LCM finds applications in algorithm design and optimization related to cyclical processes.
Understanding Divisibility Rules
Understanding divisibility rules can help simplify the process of finding the LCM, especially when dealing with larger numbers. Here are some basic divisibility rules:
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3.
- Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5.
- Divisibility by 9: A number is divisible by 9 if the sum of its digits is divisible by 9.
Advanced Methods for Larger Numbers
While the prime factorization method is efficient for relatively small numbers, more sophisticated algorithms exist for finding the LCM of larger sets of numbers, especially in computational settings. These often involve using advanced number theory concepts and data structures for optimal performance.
Conclusion: Mastering LCM Calculations
Mastering the calculation of LCMs is a valuable skill with significant applications across diverse fields. Whether you use the listing multiples method, prime factorization, or more advanced algorithms, understanding the underlying principles is key. Remember to choose the most efficient method based on the numbers involved. The examples and explanations provided in this guide will equip you with the knowledge and confidence to tackle LCM problems effectively, unlocking a deeper understanding of this fundamental mathematical concept. The LCM of 3, 9, and 15, as we've demonstrated through various methods, is unequivocally 45. This knowledge serves as a building block for more complex mathematical operations and real-world problem-solving.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 3 9 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.