Lcm Of 4 6 And 7
News Co
May 08, 2025 · 5 min read
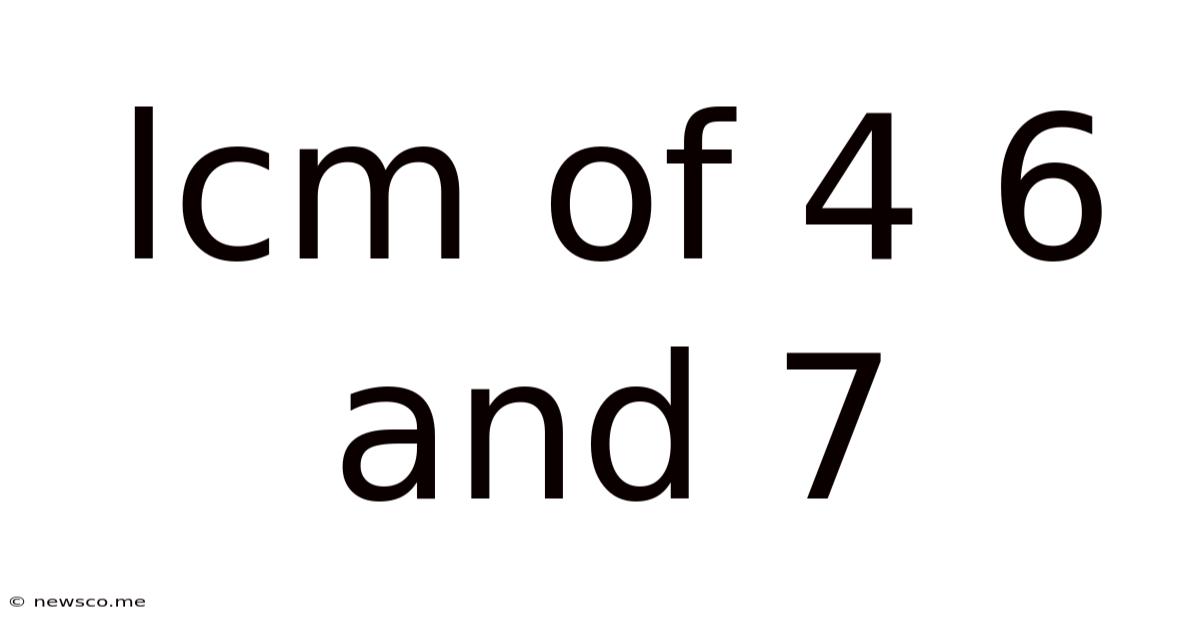
Table of Contents
Finding the Least Common Multiple (LCM) of 4, 6, and 7: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to find the LCM is crucial for various applications, from simplifying fractions to solving problems involving cycles and periodic events. This article will delve into the process of calculating the LCM of 4, 6, and 7, exploring multiple methods and providing a thorough understanding of the underlying principles. We'll also examine the broader context of LCMs and their significance in different mathematical contexts.
Understanding Least Common Multiples
Before we jump into calculating the LCM of 4, 6, and 7, let's establish a solid foundation. The LCM of a set of integers is the smallest positive integer that is divisible by all the numbers in the set. Think of it as the smallest common multiple that all the numbers share. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
This concept extends to sets of more than two numbers. Finding the LCM becomes more complex as the number of integers increases, but the fundamental principle remains the same: identify the smallest positive integer that is a multiple of all the numbers in the set.
Method 1: Prime Factorization
The most reliable and widely applicable method for finding the LCM is through prime factorization. This method involves breaking down each number into its prime factors – the smallest prime numbers that multiply together to give the original number. Let's apply this to 4, 6, and 7:
- 4: The prime factorization of 4 is 2 x 2, or 2².
- 6: The prime factorization of 6 is 2 x 3.
- 7: The prime factorization of 7 is simply 7 (as 7 is a prime number).
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2² = 4
- Highest power of 3: 3¹ = 3
- Highest power of 7: 7¹ = 7
Finally, multiply these highest powers together: 4 x 3 x 7 = 84.
Therefore, the LCM of 4, 6, and 7 is 84.
Advantages of Prime Factorization
The prime factorization method is particularly advantageous because:
- It's systematic: It follows a clear, step-by-step process that is easy to understand and replicate.
- It works for any number of integers: Whether you have two numbers or ten, the prime factorization method can be applied consistently.
- It reveals the underlying structure: It highlights the prime factors that contribute to the LCM, providing a deeper understanding of the mathematical relationships.
Method 2: Listing Multiples
A simpler, albeit less efficient method for smaller numbers, involves listing the multiples of each number until a common multiple is found. Let's try this with 4, 6, and 7:
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84...
By comparing the lists, we can see that the smallest common multiple is 84.
Limitations of Listing Multiples
This method becomes increasingly impractical as the numbers get larger. It requires a significant amount of manual calculation and increases the risk of human error. It's best suited for finding the LCM of small numbers where the common multiple is relatively easy to identify.
Method 3: Using the Formula (for Two Numbers)
For only two numbers, a formula exists that directly calculates the LCM:
LCM(a, b) = (|a * b|) / GCD(a, b)
Where:
- a and b are the two numbers
- GCD(a, b) is the greatest common divisor (GCD) of a and b. The GCD is the largest number that divides both a and b without leaving a remainder.
This formula is not directly applicable to finding the LCM of more than two numbers, however. It needs to be applied sequentially. For example, to find the LCM of 4, 6, and 7, you would first find the LCM of 4 and 6, and then find the LCM of that result and 7.
Let’s illustrate:
- Find the GCD of 4 and 6: The GCD of 4 and 6 is 2.
- Calculate the LCM of 4 and 6: LCM(4, 6) = (4 * 6) / 2 = 12
- Find the GCD of 12 and 7: The GCD of 12 and 7 is 1.
- Calculate the LCM of 12 and 7: LCM(12, 7) = (12 * 7) / 1 = 84
Applications of LCM
The concept of LCM finds application in diverse fields:
1. Fraction Simplification:
Finding the LCM is crucial for adding or subtracting fractions with different denominators. To add fractions, you need to find a common denominator, and the LCM provides the smallest possible common denominator, simplifying the calculation.
2. Cyclic Events:
LCMs are used to determine when cyclic events will coincide. For instance, if one event occurs every 4 days and another every 6 days, the LCM (84) indicates that they will occur simultaneously every 84 days. This is widely applied in scheduling and planning.
3. Gear Ratios:
In mechanical engineering, LCMs are used to calculate the optimal gear ratios in machinery. This ensures smooth and efficient operation.
4. Music Theory:
In music, LCMs help determine the least common denominator of musical rhythms and time signatures, aiding in composing harmonious melodies.
Conclusion: Mastering LCM Calculations
Finding the LCM of a set of numbers is a fundamental skill in mathematics with wide-ranging applications. While the method of listing multiples is suitable for smaller numbers, the prime factorization method offers a robust and systematic approach for any set of integers, ensuring accuracy and efficiency. Understanding the different methods allows for flexible problem-solving, depending on the complexity of the numbers involved. By mastering LCM calculations, you enhance your mathematical understanding and open doors to solving a variety of practical problems. The LCM of 4, 6, and 7, as demonstrated through several methods, is unequivocally 84. Remember to choose the method best suited to your needs and always double-check your work!
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 4 6 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.