Lcm Of 4 And 5 And 3
News Co
Mar 24, 2025 · 5 min read
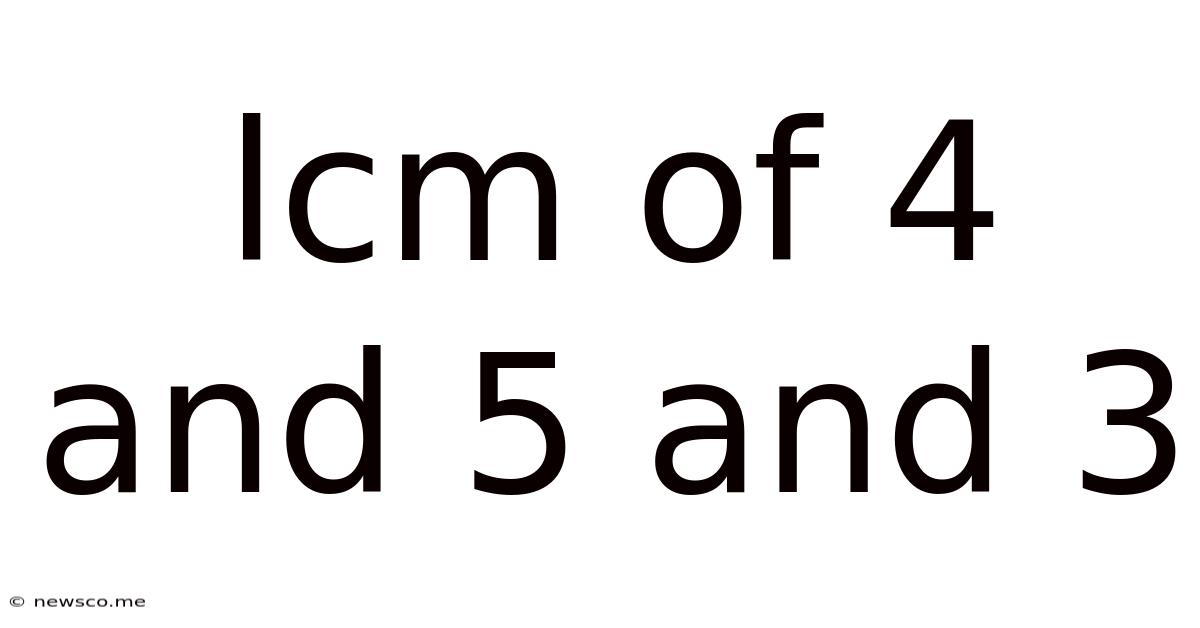
Table of Contents
Unveiling the LCM: A Deep Dive into the Least Common Multiple of 4, 5, and 3
Finding the least common multiple (LCM) might seem like a simple mathematical task, particularly with smaller numbers like 4, 5, and 3. However, understanding the underlying principles and exploring different methods for calculating the LCM lays a strong foundation for tackling more complex problems in mathematics, computer science, and even music theory. This comprehensive guide will not only show you how to find the LCM of 4, 5, and 3 but also delve into the broader concept of LCMs, exploring different approaches and practical applications.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as its factors. For instance, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18...
- Multiples of 3: 3, 6, 9, 12, 15, 18...
The common multiples of 2 and 3 are 6, 12, 18, and so on. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Finding the LCM of 4, 5, and 3: Methods and Approaches
Now, let's tackle the LCM of 4, 5, and 3. We can employ several methods:
1. Listing Multiples Method
This is a straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 30, 32, 36, 40, 44, 48, 50, 52, 56, 60...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60...
By inspecting the lists, we see that the smallest number common to all three lists is 60. Therefore, the LCM(4, 5, 3) = 60.
2. Prime Factorization Method
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
- Prime factorization of 4: 2²
- Prime factorization of 5: 5
- Prime factorization of 3: 3
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2² = 4
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Now, multiply these highest powers together: 4 * 3 * 5 = 60. Therefore, the LCM(4, 5, 3) = 60.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) are closely related. We can use the following formula:
LCM(a, b, c) = (|a * b * c|) / GCD(a, b, c)
However, this formula is most easily applicable when dealing with only two numbers, finding the GCD for three or more numbers can be tedious. While a generalized formula exists for finding the GCD of multiple numbers, the prime factorization method remains the most efficient for this scenario.
Understanding the Significance of LCM
The concept of LCM extends far beyond simple mathematical exercises. It finds practical applications in various fields:
1. Scheduling and Time Management
Imagine you have three tasks: Task A repeats every 4 days, Task B every 5 days, and Task C every 3 days. When will all three tasks coincide? The answer is the LCM(4, 5, 3) = 60. All three tasks will coincide every 60 days.
2. Music Theory
In music, LCM is crucial for understanding rhythmic patterns and finding common denominators in time signatures. For example, combining musical phrases with different lengths requires understanding their LCM to create a harmonious and balanced composition.
3. Computer Science
LCM is applied in algorithms related to cyclic events, synchronization, and scheduling processes within computer systems. Understanding the LCM helps optimize resource allocation and prevent conflicts.
4. Construction and Engineering
Calculating the LCM is essential in tasks that require precise measurements and repetition, such as designing structures with repeating patterns or planning construction projects with synchronized timelines.
5. Everyday Life
Even in everyday scenarios, LCM helps in solving problems involving cyclical events. For example, determining when to align your shopping trips to coincide with sales or when to sync your daily routines.
Beyond the Basics: Expanding LCM Calculations
While we've focused on finding the LCM of 4, 5, and 3, the principles and methods discussed apply to any set of integers. However, as the number of integers and their magnitude increase, using the prime factorization method becomes increasingly beneficial.
For example, let's consider finding the LCM of 12, 18, and 24:
- Prime factorization of 12: 2² * 3
- Prime factorization of 18: 2 * 3²
- Prime factorization of 24: 2³ * 3
The highest powers of the prime factors are: 2³ = 8, and 3² = 9. Therefore, the LCM(12, 18, 24) = 8 * 9 = 72.
Conclusion: Mastering the LCM
The least common multiple, while a seemingly simple concept, is a fundamental building block in various mathematical and real-world applications. Understanding the different methods for calculating the LCM, such as listing multiples and prime factorization, empowers you to solve diverse problems across numerous fields. This deep dive into the LCM of 4, 5, and 3 serves as a springboard for tackling more complex scenarios and appreciating the versatility of this important mathematical concept. Remember, practice is key to mastering LCM calculations and expanding your mathematical proficiency. The more you work with LCMs, the more intuitive and efficient the process will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 4 And 5 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.